Отсюда видно, что увеличение J0 приводит к
уменьшению переменной составляющей движущего момента и, следовательно,
способствует улучшению режима работы двигателя. Продифференцировав по s амплитуду каждой из гармоник ![]() , легко
убедиться, что с увеличением s каждая из этих амплитуд
возрастает; таким образом, рост крутизны характеристики двигателя вызывает
увеличение переменной составляющей движущего момента. В каталогах
электродвигателей обычно указаны номинальный момент и допустимый максимальный
движущий момент. Если исходить из допустимости двукратной перегрузки по
отношению к номинальному моменту и принять, что момент МД0(u0,w0) равен номинальному, то должно быть
, легко
убедиться, что с увеличением s каждая из этих амплитуд
возрастает; таким образом, рост крутизны характеристики двигателя вызывает
увеличение переменной составляющей движущего момента. В каталогах
электродвигателей обычно указаны номинальный момент и допустимый максимальный
движущий момент. Если исходить из допустимости двукратной перегрузки по
отношению к номинальному моменту и принять, что момент МД0(u0,w0) равен номинальному, то должно быть
![]() .
.
Влияние неравномерности вращения на потери мощности в
двигателе. Ограничимся рассмотрением роторного электродвигателя
постоянного тока с независимым возбуждением. Тогда, в соответствии с законом
Ампера 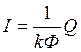 , получаем следующее выражение для силы тока
в якоре:
, получаем следующее выражение для силы тока
в якоре:
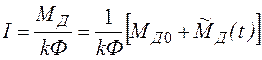 .
.
Отсюда находим среднюю за цикл мощность, теряемую в двигателе,
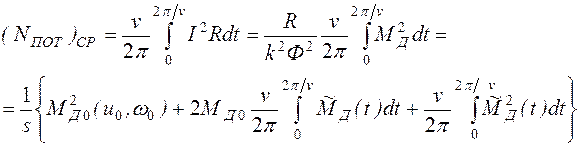 .
.
Первое слагаемое в этом выражении характеризует
мощность, теряемую в режиме равномерного вращения ротора, второе – равно нулю,
поскольку ![]() не содержит постоянной компоненты; третье
слагаемое определяет дополнительные потери, вызванные неравномерностью вращения.
Учитывая полученное выше выражение для
не содержит постоянной компоненты; третье
слагаемое определяет дополнительные потери, вызванные неравномерностью вращения.
Учитывая полученное выше выражение для ![]() , можно
представить это слагаемое в виде
, можно
представить это слагаемое в виде
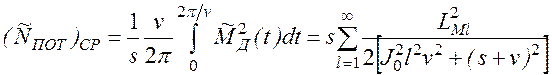 .
.
и
коэффициент потерь-![]() при
при ![]() .
.
Тогда, учитывая выражение для коэффициента неравномерности (2.47), получаем
![]()
![]() ,
,
где ![]() - коэффициент потерь в режиме равномерного
вращения с угловой скоростью
- коэффициент потерь в режиме равномерного
вращения с угловой скоростью ![]() .
.
Легко убедиться, что при большом коэффициенте
неравномерности (![]() = 0,1) и
= 0,1) и ![]() =
0,1 величина
=
0,1 величина ![]() может достигать значения 0,08, т. е.
потери мощности вследствие неравномерности вращения могут оказаться весьма
ощутимыми.
может достигать значения 0,08, т. е.
потери мощности вследствие неравномерности вращения могут оказаться весьма
ощутимыми.
2.6. Динамические нагрузки в передаточном механизме.
Определение оптимальных параметров
Определение динамического момента. Рассмотрим схему машинного агрегата (рис. 2.6), для которого дифференциальное уравнение движения машины имеет вид (2.20)
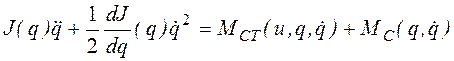 .
.
|
Рис. 2.6. Схема машинного агрегата |
Поскольку приведенные массы звеньев двигателя включены
в момент инерции J(q), под движущим моментом ![]() следует
понимать приведенный к выходному звену двигателя момент движущих сил, создаваемый
в данном случае давлением газов на поршень двигателя. Этот момент отличается от
момента МП, который будет действовать на входной вал
передаточного механизма и передаваться на остальные звенья этого механизма.
следует
понимать приведенный к выходному звену двигателя момент движущих сил, создаваемый
в данном случае давлением газов на поршень двигателя. Этот момент отличается от
момента МП, который будет действовать на входной вал
передаточного механизма и передаваться на остальные звенья этого механизма.
Для определения МП составим
уравнение движения механической системы двигателя. Для нее приведенный момент
инерции равен JД(q), движущий момент совпадает с ![]() ,
а момент сил сопротивления равен - МП. Поэтому уравнение
движения записывается в форме уравнения Лагранжа следующим образом:
,
а момент сил сопротивления равен - МП. Поэтому уравнение
движения записывается в форме уравнения Лагранжа следующим образом:
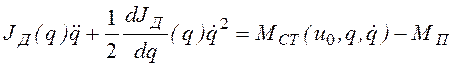 .
.
Перепишем это уравнение в форме, аналогичной (2.28).
Учитывая, что ![]() , получим
, получим
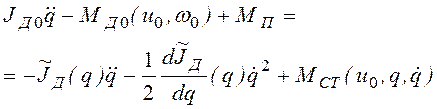 .
.
Подставив в левую часть ![]() , а в
правую -
, а в
правую - ![]() и линеаризуя функцию МД0,
найдем
и линеаризуя функцию МД0,
найдем
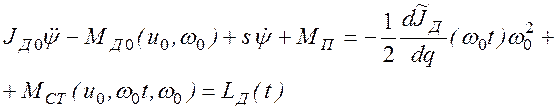 .
.
Отсюда
![]() . (2.49)
. (2.49)
Первое слагаемое в правой части (2.49) представляет собой постоянную составляющую момента МП, равную среднему приведенному моменту сил сопротивления; остальные слагаемые составляют переменный динамический момент в передаточном механизме
![]() . (2.50)
. (2.50)
Из уравнения (2.44) следует, что
![]() .
.
Подставив это выражение в (2.50), найдем
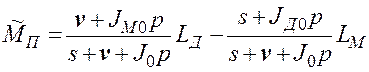 . (2.51)
. (2.51)
Таким образом, определились передаточные функции
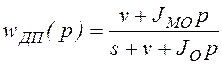 ;
; 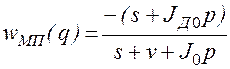 ,
,
связывающие динамическую составляющую момента ![]() с
возмущениями LД и LМ.
с
возмущениями LД и LМ.
Переходя от передаточных функций к частотным характеристикам и подставляя в (2.51) разложения (2.36) и (2.38), находим
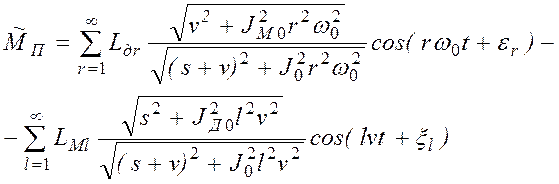 , (2.52)
, (2.52)
где ![]() ;
; ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.