Механика \ Динамика машин

Динамика жесткой машины с одной степенью подвижности, страница 21

где      - угол между линией действия силы N и осью х; r - радиус цапфы.

 


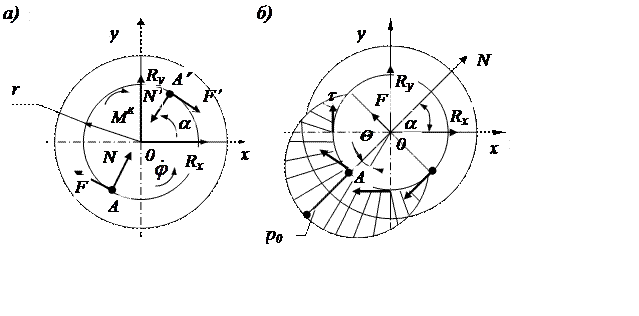Рис. 2.15. Модели трения вращательной пары

В формулах (2.95) учтено, что с изменением знака N меняется направление силы F, поскольку точка ее приложения из A смещается в .

В модели, показанной на рис. 2.15,б, предполагается, что силы нормального взаимодействия распределены по полуокружности с серединой в точке А. Обычно закон распределения выбирают в форме

,

где р - давление в сечении, составляющем угол  с радиусом OA.

Силы трения также являются распределенными, касательное напряжение , в соответствии с законом Амонтона-Кулона, выбирается пропорциональным р. Проецируя распределенные силы на направление радиуса ОА и перпендикулярное к нему, а также определяя их момент относительно точки О, находим:

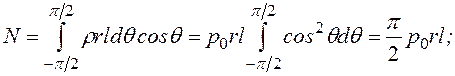
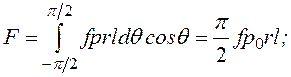
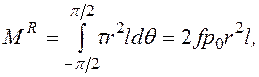
где      - длина образующей цапфы.

Отсюда получаем:

 

(2.96)
 

.

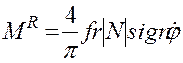Сравнивая эти выражения с (2.95), замечаем, что они отличаются лишь увеличением в  раз момента сил трения. Первая модель обычно используется при расчете кинематических пар со значительными зазорами (например, изношенных).

Червячная  передача. На рис. 2.16 схематично представлены силы, возникающие в червячной передаче. Предполагается, что рабочие поверхности витка червяка и зуба червячного колеса контактируют в точке В. Нормальная сила N (на рисунке показана сила, действующая на колесо) составляет угол  с плоскостью, параллельной оси колеса;  - угол подъема витка на червяке. Сила трения F направлена  противоположно  скорости скольжения.

Проецируя силу взаимодействия R на оси координат, находим окружную силу S и осевую силу Р на колесе.

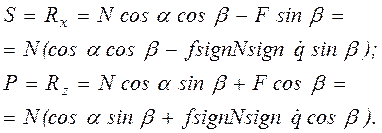                                                                                                                (2.97)

         X          N                     N       M1

                                        R

                                                            S

Y  M2                           B                                      

                                          P               B

r2                          r1                   F


                                                     

Рис. 2.16. Модель трения червячной передачи

Сила N может изменять направление на противоположное при изменении направления момента М2, приложенного к колесу (на рисунке показан случай, когда этот момент направлен против вращения колеса). Направление силы F изменяется только при изменении знака угловой скорости червяка .

2.11. Исследование разбега машины

Определение закона движения. В процессе разбега угловая скорость выходного звена двигателя изменяется от  = 0 до = (значение, соответствующее средней угловой скорости установившегося движения). Закон движения машины при разбеге является решением уравнений движения, соответствующим начальным условиям t = 0, = 0. Начальное значение координаты q обычно является неизвестным, оно мало влияет на  закон изменения угловой скорости и может, поэтому, задаваться произвольно [например, q (0) = 0]. Задав начальные условия, мы сводим задачу исследования к классической задаче Коши, решение которой может быть получено численным интегрированием на ЭВМ с помощью метода Рунге-Кутта или других численных методов.

Однако при численном решении задачи трудно оценить влияние отдельных параметров на динамические характеристики, что необходимо для задач динамического синтеза. Поэтому здесь остановимся на некоторых аналитических подходах к решению задачи разбега машины. Будем рассматривать неуправляемый разбег агрегата, когда u (t) = u0 = constпри t>0. Иными словами, речь пойдет о разбеге машины при подаче на вход двигателя постоянного значения u.

Скачать файл