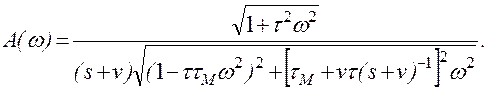Динамика жесткой машины с одной степенью подвижности, страница 18

                                                                                                                (2.90)

Ограничимся описанием лишь некоторых наиболее существенных особенностей, отражающих влияние постоянной времени t.

Обычно в машинных агрегатах <<. На этом основании пренебрежем в знаменателе (2.90) слагаемым  tv (s + v)^-1 . Построим график функции (s + v) А(w); его форма будет зависеть от отношения . Определим значение w=w*, отличное от нуля, при котором  имеет максимум. Приравнивая нулю производную , находим

.

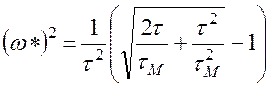Вещественное значение для  получается при

>1

или при

>.

На рис. 2.11 показаны типичные формы АЧХ при < 0,41 и при >0,41. В последнем случае на частоте  наблюдается увеличение амплитуды; это явление принято называть двигательным резонансом.

Аналитическое выражение для :

.

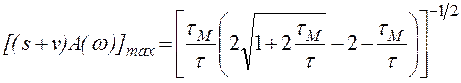Значения  и  при различных :

                       0,41         0,500       1,000       2,000       4,000

                        0              0,343       0,856       1,352       1,975

       1              1,029       1,468       2,468       2,478

>0,41        2                              <0,41                                                          1               0                                     Рис. 2.11. Амплитудно-частотные характеристики для ошибки по угловой скорости

Отметим, что зависимость  от  не является монотонной. Дифференцируя выражение (2.90) по  и приравнивая нулю производную, можно определить значение  соответствующее максимуму

.

(Здесь по-прежнему предполагается, что >>). Если <, то увеличение среднего момента инерции машины J₀ приведет к увеличению , поскольку при этом возрастет . Значит, возрастет гармоника частоты  в , а, следовательно, и неравномерность вращения ротора двигателя. Таким образом, увеличение среднего момента инерции (установка маховика) может приводить к увеличению неравномерности вращения.

Из изложенного следует, что возможность использования статической характеристики двигателя при исследовании установившихся движений обуславливается, в первую очередь, величиной отношения .  При > 0,41 необходимо пользоваться динамической характеристикой; в противном случае можно не обнаружить двигательный резонанс, то есть  получить   неверные  качественные представления о характере динамических процессов. Кроме того, определив динамическую составляющую движущего момента  из (2.87), полезно сравнить ее с ; если при заданных возмущениях >, использование статической характеристики может приводить к большим количественным ошибкам. Если в возмущении L_М превалирует первая гармоника, а , то условие допустимости использования статической характеристики принимает форму
<< 1.

Динамический момент в передаточном механизме. Определим  переменную составляющую момента в передаточном механизме, предполагая, что L¢_Д(t) = 0; . Второе уравнение (2.87) дает при этом

.

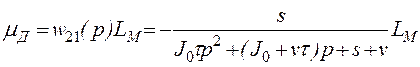Переменную часть момента в передаточном механизме найдем из уравнения движения ротора, имеющего постоянный момент инерции (поскольку ):

,

или

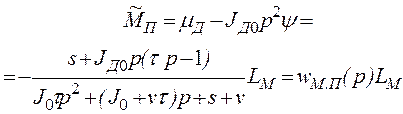.                                                                                                                (2.91)

Подставляя L_M(t)  из (2.38), находим

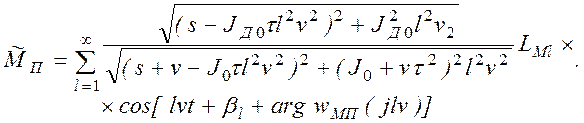
Анализируя соответствующую АЧХ при t_М  >>vt(s+v)^-1

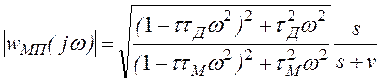,                     (2.91,а)

где  -  механическая постоянная времени двигателя, можно показать, что экстремумы  достигаются при

±

±.

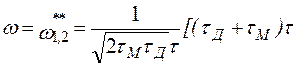Меньшее из двух значений  существует лишь в том случае, если t_Д + t_М < 2t. Далее можно установить, что при t_Д >t_М меньшее значение w** соответствует минимуму, а большее - максимуму     |v_М.П.(jw)|. При t_Д <t_М имеет место противоположная ситуация. Если же t_Д = t_М, то из (2.91а) следует, что

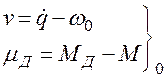         малые вариации

 (Естественно, что все это справедливо, если >>vt (s+v)^-1). Легко показать также, что

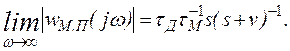
На рис. 2.12 показаны АЧХ, соответствующие различным соотношениям между постоянными времени t_Д, t_М, t. Здесь же нанесены АЧХ, соответствующие t = 0.