Динамика жесткой машины с одной степенью подвижности, страница 3

Другое уравнение движения машины — это одна из характеристик двигателя, рассмотренных в п. 2. Предполагая в дальнейшем, что выходное звено двигателя совершает вращательное движение, будем записывать характеристики двигателя в следующем виде:

а) идеальную кинематическую характеристику - в виде ;

б) статическую характеристику  - в виде

;                                                                                                                   (2.16)

в) динамическую характеристику  - в виде

.                                                                                                                   (2.17)

Будем предполагать, что осуществляется программное управление движением машины. Тогда входной параметр u является заданной функцией времени. В частном случае, при неуправляемой машине,
u = u₀ =  const.

Функция M_СТ в ряде случаев не зависит от координаты q (например, для роторных электрических двигателей), в других случаях она является периодической функцией угла поворота, период которой зависит от цикла двигателя. Условимся выбирать q таким образом, чтобы цикл двигателя соответствовал изменению q на 2p; тогда таким же окажется и период функции М_СТ. Например, в четырехтактных двигателях внутреннего сгорания, в которых полный цикл происходит за два оборота коленчатого вала, величина q должна равняться половине угла поворота выходного звена.

Как периодическую функцию М_СТ можно представить в виде

,                                                                                                                   (2.18)

где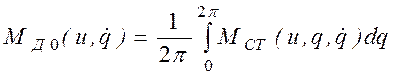                  

будем называть средним моментом движущих сил. Для роторных двигателей .

Если в качестве динамической модели двигателя выбрана его идеальная кинематическая характеристика (1.2), закон изменения  q(t) определяется непосредственно по этой характеристике как интеграл:

.

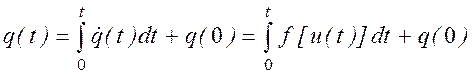Уравнение (2.12) в этом случая для определения закона изменения движущего момента М_Д(t) будет иметь вид

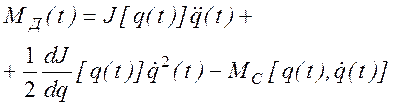.                                                                                                                   (2.19)

Подставляя в (2.15) статическую характеристику двигателя (2.16), получаем дифференциальное уравнение движения машины

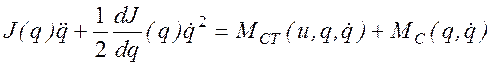,                                                                                                                   (2.20)

содержащее одну неизвестную функцию времени q. Таким образом, в этом случае задача динамического анализа сводится к интегрированию уравнения (2.20) при заданной функции u(t).

Наконец, в случае использования динамической характеристики двигателя задача сводится к интегрированию системы двух дифференциальных уравнений (2.15) и(2.17)c двумя неизвестными q(t) и М_Д(t).

Выбор той или иной характеристики двигателя зависит в первую очередь от задачи исследования, а также от характера исследуемого режима движения машины.

Режимы движения. Исследование динамики машины заключается в первую очередь в определении и анализе частных решений полученных   дифференциальных уравнений движения, соответствующих некоторым характерным режимам работы. Перечислим эти режимы.

Установившееся движение. Понятие «установившееся движение» трудно поддается точному определению. Этот режим движения характерен для машин, в течение продолжительного времени выполняющих циклически повторяющийся рабочий процесс или работающих в статическом режиме, при котором параметры рабочего процесса и, в частности, силы полезного сопротивления остаются постоянными. В установившемся режиме угловая скорость выходного звена двигателя часто является периодической функцией времени, однако периодичность процесса движения не обязательно свидетельствует о его установившемся характере. Например, цикловой режим работы станка, состоящий из таких этапов, как установка детали на станок, при которой рабочие органы его неподвижны, и обработка детали, в процессе которой рабочие органы и выходные зренья двигателей движутся с резко изменяющимися скоростями, вряд ли целесообразно считать установившимся движением.