Динамика жесткой машины с одной степенью подвижности, страница 20

                              0

Рис. 2.13. Силы трения в кинематической паре

В высшей кинематической паре наряду с трением скольжения возникают трение качения и трение верчения, которым соответствуют элементарные моменты сил взаимодействия: момент трения качения dМ_К, лежащий в касательной плоскости, и момент трения верчения dМ_В, направленный по нормали. При анализе динамики механизмов эти моменты обычно не учитываются.

Выбор динамической модели кинематической пары связан в первую очередь с заданием закона трения, т.е. зависимости сил и моментов сил трения от нормальной силы  и скорости скольжения . Силу трения скольжения чаще всего описывают законом Амонтона-Кулона, согласно которому модуль силы трения пропорционален модулю. Таким образом, можно принять, что

.

Коэффициент трения f, строго говоря, зависит от скорости скольжения. При относительном покое  коэффициент f  может принимать любое значение, не превосходящее некоторого f₀, называемое коэффициентом трения покоя. В широком диапазоне значении скорости скольжения коэффициент трения может считаться постоянным (несколько меньшим, чем f₀), что и будет приниматься в дальнейшем.

Для низших кинематических пар выбор модели трения предполагает также задание закона распределения нормальных сил по поверхности соприкосновения звеньев. Определение этого закона является сложной задачей, решение которой требует рассмотрения динамической модели кинематической пары, учитывающей наличие зазоров, смазочного слоя и т.п. Чтобы избежать этого, обычно делают некоторые достоверные предположения о характере распределения нормальных сил по поверхности и, исходя из них, выражают силы трения через остальные компоненты реакций. Рассмотрим некоторые наиболее типичные модели трения.

Поступательная пара. Предполагая, что поступательная пара принадлежит плоскому механизму, зададим только компоненты реакций, лежащие в плоскости движения.

Простейшая модель представлена на рис. 2.14,а. Предполагается, что нормальные силы взаимодействия сводятся к сосредоточенной силе N, приложенной в некоторой точке А ползуна, если соприкосновение его происходит с нижней направляющей. При изменении действующих сил возможна перекладка зазоров, т.е. переход к соприкосновению с верхней направляющей. При этом направление нормальной реакции изменяется на противоположное (N'), а точка приложения переходит в . Сила трения  направлена против скорости движения  (на рисунке принято, что
х > 0). Проецируя силы на оси и определяя их моменты относительно начала координат О, получаем компоненты реакции, лежащие в плоскости движения:

                                                                                                                   (2.93)

Здесь учтено, что при изменении знака N изменяется и знак момента, создаваемого силой F.

Более сложная модель, учитывающая возможность перекоса ползуна и одновременного соприкосновения его с обеими направляющими, представлена на рис. 2.14,б. Здесь нормальные реакции сведены к силам , приложенным  в точках А и В. В этом случае получаем:

.                                                                                                                (2.94)

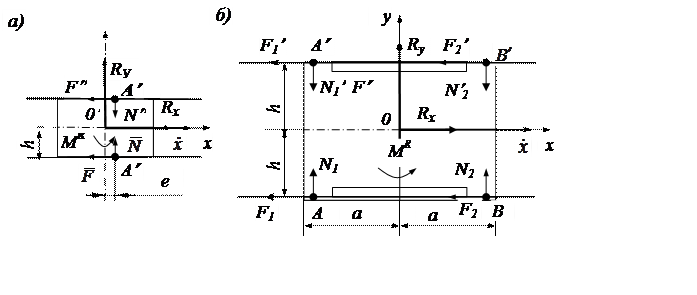Рис. 2.14. Модели трения поступательной пары

Первая модель (рис. 2.14,а) используется обычно для ползуна, геометрические размеры которого достаточно малы по сравнению с другими линейными параметрами механизма; для ползуна больших размеров используется вторая модель.

Вращательная  пара. На рис. 2.15 представлены модели трения вращательной пары плоского механизма. В модели, представленной на рис. 2.15,а, предполагается, что силы нормального взаимодействия звеньев сосредоточены в точке А() и в той же точке приложена сила трения F. Проецируя силы на оси и определяя их моменты, находим

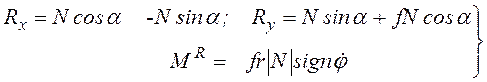                                                                                                                                                                                                                               (2.95)