|
Исследование собственных колебаний круглой однородной пластины, защемлённой по внешнему контуру |
|
Задание: в соответствии с вариантом задания определить три первые формы и частоты собственных колебаний пластины. |
|
Исходные данные: |
|
Внешний радиус, м: |
|
|
|
Толщина пластины, м: |
|
|
|
Плотность материала, кГ/м^3: |
|
|
|
Модуль упругости Е, Н/м^2: |
|
|
|
Коэффициент Пуассона: |
|
|
|
Цилиндрическая жесткость, Н*м: |
|
|
|
|
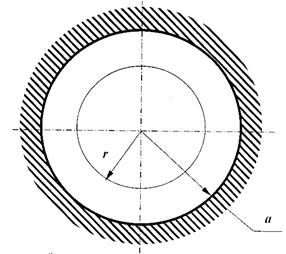
Рис. 1 – Схема закрепления пластины (к л.р. 14)
|
Собственные колебания круглой однородной пластины описы- ваются дифференциальным уравнением: |
|
|
|
|
|
- прогиб пластины |
|
Функции Бесселя: |
|
|
|
- функция Бесселя 1-го рода нулевого порядка |
|
|
|
- модифицированная функция Бесселя 1-го рода нулевого порядка |
|
Решение этой задачи записывается в виде: |
|
|
|
|
|
- собственные значения |
|
|
|
- собственные частоты |
|
Коэффициент А, определяемый из начальных условий примем равным 1. |
|
|
|
- Г-функция |
|
Производные от Бесселевых функций: |
|
|
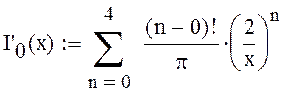
|
Определим коэффициенты ki, записав систему уравнений в матричной форме: |
|
|
Приравняв определитель матрицы нулю, получаем собственные значения ki.
|
Итак, собственные значения: |
|
|
|
собственные частоты: |
|
|
|
|
|
Исследование собственных колебаний круглой однородной пластины с отверстием по центру, защемлённой по внутреннему контуру |
|
Задание: в соответствии с вариантом задания определить три первые формы и частоты собственных колебаний пластины. |
|
Исходные данные: |
|
Внутренний радиус, м: |
|
|
|
Внешний радиус, м: |
|
|
|
Толщина пластины, м: |
|
|
|
Плотность материала, кГ/м^3: |
|
|
|
Модуль упругости Е, Н/м^2: |
|
|
|
Коэффициент Пуассона: |
|
|
|
Цилиндрическая жесткость, Н*м: |
|
|
|
|
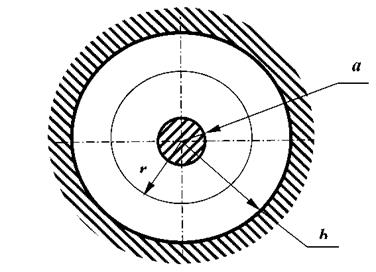
Рис. 2 – Схема закрепления пластины (к л.р. 12)
|
Собственные колебания круглой однородной пластины описы- ваются дифференциальным уравнением: |
|
|
|
|
|
- прогиб пластины |
|
Функции Бесселя: |
|
|
|
- функция Бесселя 1-го рода нулевого порядка |
|
|
|
- функция Бесселя 2-го рода нулевого порядка |
|
|
|
- модифицированная функция Бесселя 1-го рода нулевого порядка |
|
- модифицированная функция Бесселя 2-го рода нулевого порядка |
|
|
|
Решение этой задачи записывается в виде: |
|
|
Коэффициент А, определяемый из начальных условий примем равным 1.
Из начальных и граничных условий нашли В=-1, С=D=0.
|
Определим коэффициенты ki, записав систему уравнений в матричной форме: |
|
|
Приравняв определитель матрицы нулю, получаем собственные значения ki.
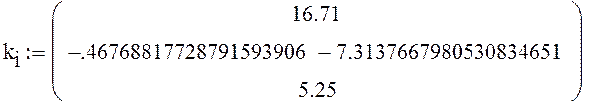
|
собственные частоты: |
|
|
|
|
|
Исследование собственных колебаний круглой однородной пластины с отверстием по центру, защемлённой по внутреннему и внешнему контуру |
|
Задание: в соответствии с вариантом задания определить три первые формы и частоты собственных колебаний пластины. |
|
Исходные данные: |
|
Внутренний радиус, м: |
|
|
|
Внешний радиус, м: |
|
|
|
Толщина пластины, м: |
|
|
|
Плотность материала, кГ/м^3: |
|
|
|
Модуль упругости Е, Н/м^2: |
|
|
|
Коэффициент Пуассона: |
|
|
|
Цилиндрическая жесткость, Н*м: |
|
|
|
|
|
Собственные колебания круглой однородной пластины описываются дифференциальным уравнением: |
|
|
|
|
|
- прогиб пластины |
Функции Бесселя:
|
|
|
- функция Бесселя 1-го рода нулевого порядка |
|
|
|
- функция Бесселя 2-го рода нулевого порядка |
|
|
|
- модифицированная функция Бесселя 1-го рода нулевого порядка |
|
- модифицированная функция Бесселя 2-го рода нулевого порядка |
|
|
|
Решение этой задачи записывается в виде: |
|
|
Коэффициенты А и С, определяемый из начальных условий примем равным 1 и 1,5.
|
Определим коэффициенты ki, записав систему уравнений в матричной форме: |
|
|
|
Итак, собственные значения: |
|
|
|
собственные частоты: |
|
|
|
|
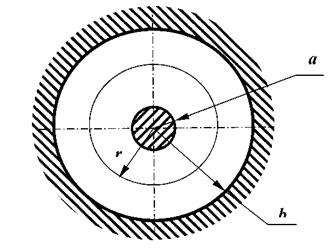
Рис. 3 – Схема закрепления пластины (к л.р. 13)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.