Составление уравнений движения тела и определение реакций опор

Рассматривается разгон компрессора

Дано: м м м м м м рад кг кг Н∙м∙с2 Н∙м∙с2  Н∙м с-1  с

Требуется:

- составить уравнения вращательного движения ротора и уравнения для определения динамических реакций в подшипниках;

- определить координаты центра масс ротора и его матрицу инерции, с помощью ПК проинтегрировать уравнения движения для заданных начальных условий на интервале времени τ и   определить изменение во времени динамических реакций;

- построит графики ωz(t),  εz(t),  RA(t),   RB(t) для момента времени

t* = Δt (N+1), изобразить векторы динамических реакций на схеме ротора.

Решение:

Физико-математическая модель

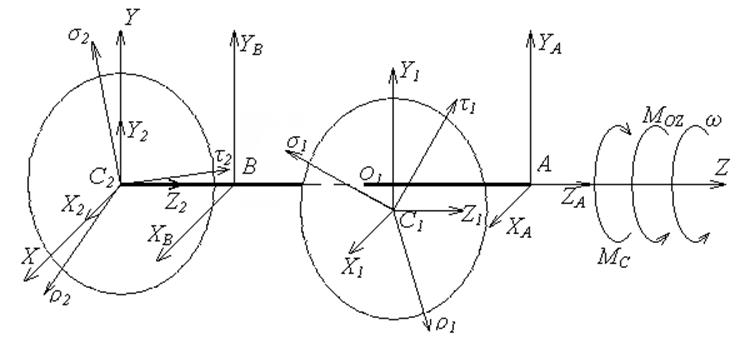
Вращающий  момент         

Момент сопротивления     

Mq – вращающий момент,

Mo – движущий момент,

Mс – момент сопротивления,

r₂s₂t₂ - главные центральные оси инерции колеса 2,

w - угловая скорость ротора,

Y_B, X_B, X_A, Y_A- составляющие реакций отброшенных связей

Воспользуемся теоремами об изменении количества движения и кинетического момента относительно точки А  и В .

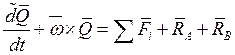
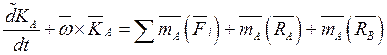
m- масса элементов системы.

, -реакции отброшенных связей

При выборе варианта необходимо руководствоваться следующим:

Массы первого и второго дисков:

Коэффициенты

Момент привода

Момент сопротивления

Вычислим инерционно-массовые характеристики ротора. Массу ротора определяем как сумму масс его элементов.

Координаты центров масс элементов(колёс) в системе координат AXYZ

Координаты центра масс ротора:

                           

                     

                   

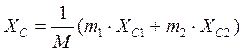
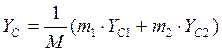
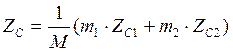
Далее вычисляем моменты инерции ротора, относительно связанной с ним системы координат AXYZ ,т.е. определим матрицу составляющих тензора инерции

    

Так как главные центральные оси первого колеса повёрнуты вокруг оси y₂  на малый угол β, то

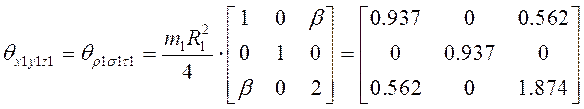
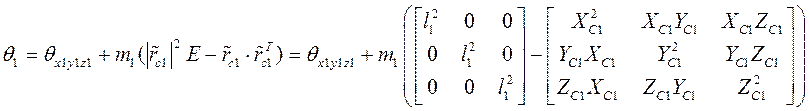
 единичная матрица размера 3 ×3

 квадрат длины вектор- столбца 

 его матрица рассеивания

                            

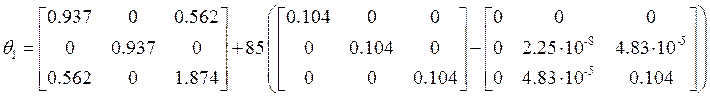
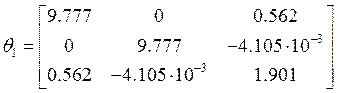
Так как главные центральные оси второго колеса повёрнуты вокруг оси y₂  на малый угол α ,то

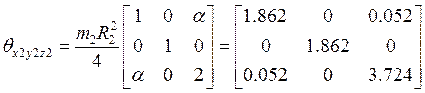
и матрица инерции  второго колеса определиться как

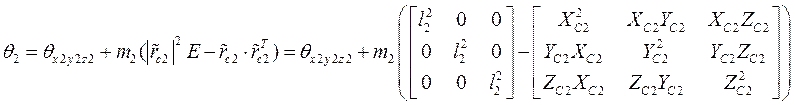
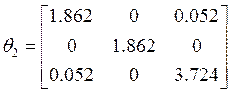
матрица инерции ротора

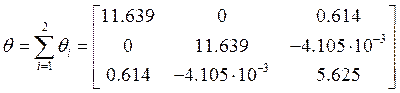
откуда выписываем все моменты инерции ротора

Составление уравнений движения

Дифференциальное уравнение вращательного движения ротора и уравнения для определения динамических реакций в подвижных осях имеют вид:

 

Так как, а получаем

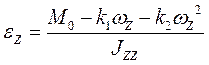
Подставив в эти уравнения численные значения и решив их, получим выходные параметры:

Рассмотрим временной интервал

Количество участков интегрирования

Результаты счета:

 

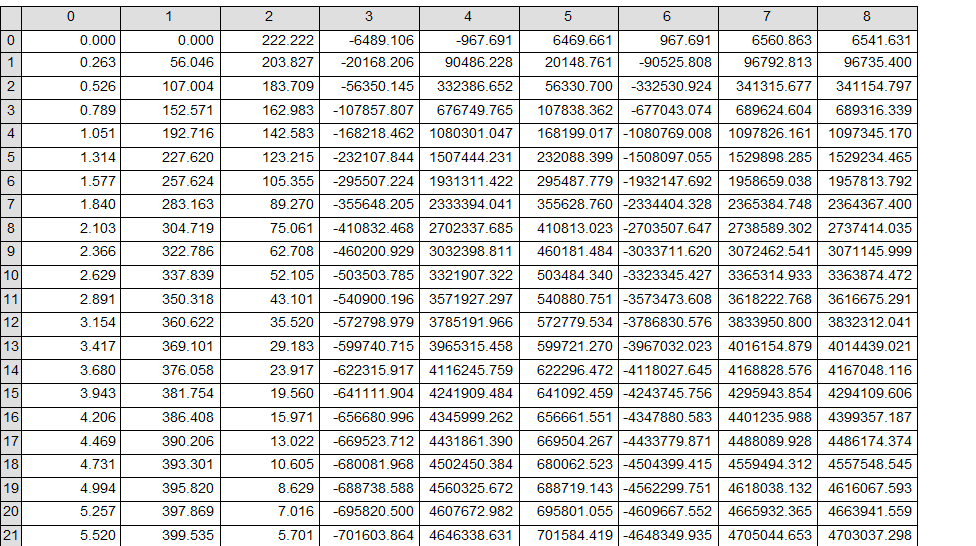
Найдём угловую скорость установившегося вращения

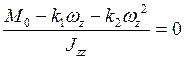
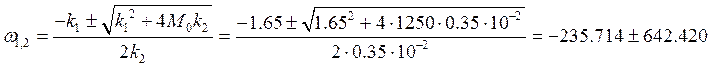
как по условию работы ротор не изменяет направления вращения, то в качестве установившегося значения угловой скорости возьмём положительное

ω = 406.7 с^-1

График изменения угловой скорости у углового ускорения

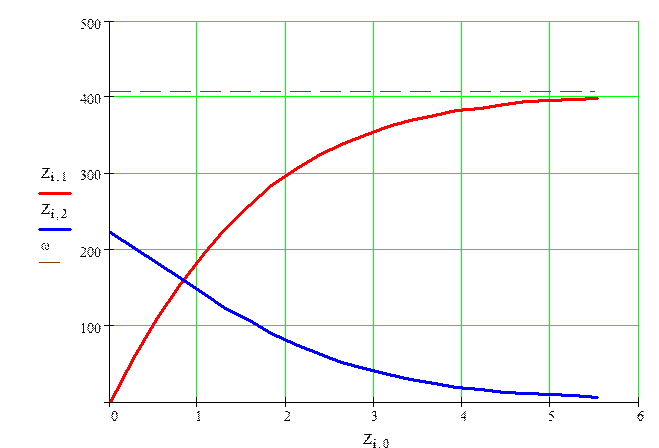
Угловая скорость

 Угловое ускорение

w - Угловая скорость установившегося вращения

График изменения реакцийи

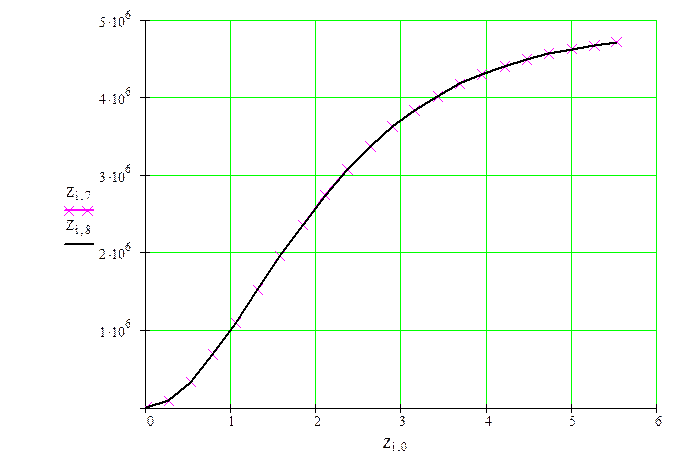
Опорная реакция в точке А

 Опорная реакция в точке В

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение

Высшего профессионального образования

«Комсомольский – на – Амуре государственный технический университет»

Кафедра «Теоретическая и прикладная механика»

Расчетно – графическое задание №1

Составление уравнений движения тела

и определение реакций опор

Выполнила Романченко В.Н.

Проверил Шарлаимов В.И.

Группа 2 Дм – 1

Комсомольск – на – Амуре

2006г.