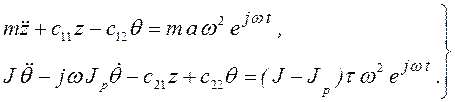Устойчивость колебаний. Общая постановка и критерии устойчивости линейных систем. Специальные приемы исследования устойчивости

.                                                                                                                 (3.119)

Движение диска определяется решением этих уравнений

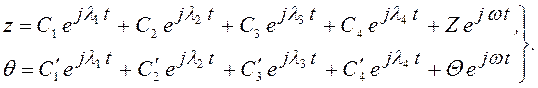                                                                                                                 (3.120)

Движение состоит из собственных прецессий центра диска и угловых прецессий плоскости диска с частотами λ₁, λ₂, λ₃, λ₄, а также из вынужденных аналогичных прецессий с частотой ω вращения.

Глава 4. УСТОЙЧИВОСТЬ  КОЛЕБАНИЙ

4.1. Общая  постановка и критерии устойчивости 

линейных систем

Устойчивость колебаний есть частный случай устойчивости движения вообще. Под устойчивостью движения по А.М. Ляпунову, которому мы обязаны созданием общей теории устойчивости движения, понимают свойство движения системы, характеризующееся тем, что отклонения ее от данного движения или иные величины, зависящие от отклонений, могут быть достаточно малыми, если соответственно малы начальные возмущения, т. е. малы изменения условий движения в начальный момент.

Строгая математическая формулировка этого определения связана с понятием устойчивости решений системы дифференциальных уравнений движения.

Пусть имеем систему обыкновенных дифференциальных уравнений

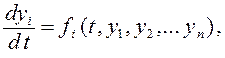                                                                                                                                                                                (4.1)

где    дf_i /дy_k ( k = 1, 2, …, n) существуют и непрерывны, и пусть φ_i (t)
(i = 1, 2, …, n) есть решение этой системы, удовлетворяющее при t=t₀   условиям

.

Решение  φ_i (t) системы (4.1) называют устойчивым, если для любого
ε > 0 можно подобрать δ(ε) > 0 такое, что для всякого решения y_i (t) системы (4.1), начальные значения которого y_i (t₀)  удовлетворяют условию

| y_i (t₀) – φ_i⁰ | > δ (ε) ,                                                         (4.2)

для всех   справедливы неравенства

| y_i (t) – φ_i (t) | < ε .                                                                                                                     (4.3)

Если при сколь угодно малом δ(ε) > 0 хотя бы для одного решения y_i(t) неравенства (4.3) не выполняется, то решение, определяемое функцией φ_i(t) называют неустойчивым.

Вопрос об устойчивости решения может быть сведен к вопросу устойчивости нулевого решения x₀(t) некоторой новой системы уравнений, получающейся из (4.1) линейной заменой функций

x_i(t) = y_i(t) – φ_i(t).                                                                                                                      (4.4)

При такой постановке исследуется нулевое решение x_i (t) = 0  или расположенная в начале координат точка покоя соответствующей системы дифференциальных уравнений.

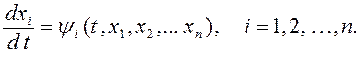                                                                                                                     (4.5)

Применительно к точке покоя x_i (t) = 0 условие устойчивости формулируется так.

Решение в точке покоя x_i(t) = 0  устойчиво, если для каждого
ε > 0 можно подобрать δ(ε) > 0  такое, что из неравенства x_i(t₀) > δ(ε) следует неравенство

| x_i(t) | < ε                                                                                                                     (4.6)

при > t0

Устойчивость или неустойчивость решения системы дифференциальных уравнений характеризует устойчивость или не устойчивость движения, определяемого этим решением.

Вместо устойчивости движения в окрестности той или иной точки говорят об устойчивости системы в этой точке или об устойчивости самой точки. Так, уже говорилось об устойчивости или неустойчивости нулевой точки – фокуса при изображении движения на фазовой плоскости.

Для частного случая движения – колебания – требования к устойчивости в определениях не отличаются от сформулированных выше.

В сущности, неустойчивость многих видов движения проявляется в том, что система начинает колебаться относительно заданного движения; точки системы совершают колебания (приближенно гармонические) относительно их траекторий, соответствующих номинальному движению, и это колебательное движение происходит с нарастающей во времени амплитудой. Поэтому исследование устойчивости заданного движения во многих случаях можно вести по этой схеме, а именно: изучать вопрос о том, будут ли колебания относительно этого движения иметь нарастающие или убывающие во времени амплитуды.

В такой ограниченной постановке изучается устойчивость колебаний

линейных систем, а также устойчивость нелинейных систем по первому приближению, которое состоит в замене данной системы близкой ей линейной системой. В ряде случаев (сюда не относятся особые случаи, частично рассмотренные Ляпуновым) решение вопроса устойчивости по первому приближению оказывается достаточным для решения вопроса об устойчивости движения системы вообще.