Устойчивость колебаний. Общая постановка и критерии устойчивости линейных систем. Специальные приемы исследования устойчивости, страница 4

Построение указанной геометрической характеристики дает возможность проверить, устойчива ли заданная система. При проектировании представляет практический интерес возможность подбора параметров системы из условий устойчивости.

Это достигается  применением способов построения  границы час-

тей устойчивости и неустойчивости в системе координат, зависящих от параметров системы.

Пусть устойчивость определяется знаками вещественных частей корней алгебраического уравнения

                                                                                                                                                                             (4.25)

Вместо того, чтобы рассматривать комплексную плоскость корней
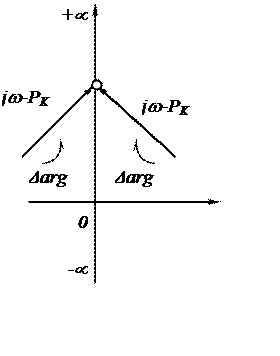
α_k + β_k, рассмотрим многомерное пространство вещественныx коэффициентов а₀, а₁… а_п. Заменив р на jω  заставим ω пробегать все вещественные значения от –∞ до +∞. Это будет соответствовать чисто мнимым значениям р, т. е. точкам мнимой оси корней р₁, р₂, …р_n,иными словами, границе устойчивости. При этом уравнение, полученное заменой (4.25) р на jω,

                                                                                                                                                                             (4.26)

можно представить себе как уравнение гиперповерхности в пространстве коэффициентов а₀, а₁… а_п. Вещественным значениям параметра ω  будет соответствовать гиперповерхность, которая является границей между областью устойчивости и областью неустойчивости.

Чтобы не иметь дела  с многомерным пространством, можно полагать сперва, что изменяются  только два каких-нибудь коэффициента, например а₀ и а₁, а остальные постоянные; далее можно полагать   изменяющимися коэффициенты а₀ и а₃, и т.д. Каждый раз имеем плоскость с координатами а₀ и а_k, и в этой плоскости граница устойчивости будет представлять некоторую   кривую   линию, отображающую мнимую ось комплексной плоскости α_k + jβ_k. Не представляет труда установить, какая из областей будет областью устойчивости и какая областью неустойчивости. В самом деле, на комплексной плоскости α_k + jβ_k , если двигаться вдоль мнимой оси от –∞j до +∞j, область  устойчивости расположена слева от оси, поэтому в плоскости параметров (а₀, а_k) область устойчивости должна располагаться слева, если двигаться в сторону увеличивающихся значений ω.

Область устойчивости можно строить не только в пространстве коэффициентов а₀, а₁… а_п, но и в пространстве других параметров, зависящих от этих коэффициентов или входящих в них, если они заданы алгебраическими выражениями.

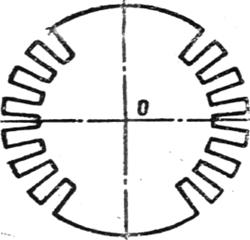
Рассмотрим пример построения области устойчивости колебаний двухопорного гибкого вала с диском посредине, имеющего поперечное сечение неравно-жесткое в двух главных направлениях изгиба. Сечение такого вала показано на рис. 4.3.

Для составления дифференциальных уравнений колебаний такого вала применим систему координат, вращающуюся вместе с валом с угловой скоростью ω. Кинетическая и потенциальная энергия системы, а также диссипативная функция при изгибных колебаниях вала будут соответственно

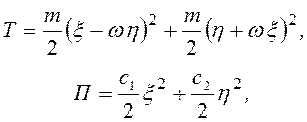
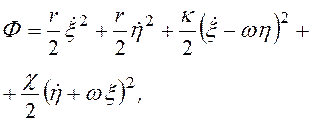   (4.27)

где     c₁ = 48EJ₁/l³и c₂ = 48EJ₂/l³−коэффициенты двух главных жесткостей на изгиб; J₁, J₂−главные экваториальные моменты инерции сечения вала;
χ, r − коэффициенты внешнего и внутреннего трения.

Вставив  (4.27) в уравнения Лагранжа, получим дифференциальные уравнения изгибных колебаний вала

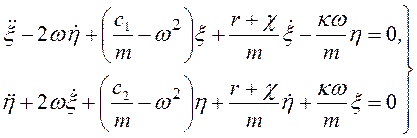.                                                                                                                   (4.28)

Полагая решение в виде , придем к следующему характеристическому уравнению