Устойчивость колебаний. Общая постановка и критерии устойчивости линейных систем. Специальные приемы исследования устойчивости, страница 2

Ограничимся здесь кратким рассмотрением устойчивости систем, описываемых линейными дифференциальными уравнениями.

Известно, что механические колебательные системы описываются дифференциальными уравнениями второго порядка, в частности линейными. Последние имеют общий вид

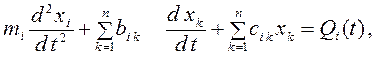                                 (4.7)

где    x_i – отклонение системы от положения равновесия или от некоторого движения.

Общее решение системы имеет вид

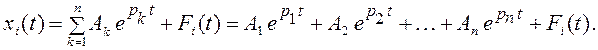          (4.8)

Здесь F_i(t) – частное решение системы (4.7), а функции  – фундаментальные решения системы дифференциальных уравнений без правой части

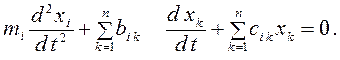                                                                          (4.9)

Числа  - корни алгебраического уравнения частот

. (4.10)

Корни алгебраического уравнения  комплексны и могут быть представлены в виде

                                                                                                                                                                           (4.11)

а общее решение (4.9), выражающее собственные колебания, представляется таким образом

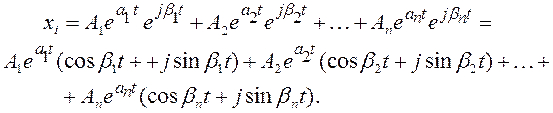                                                                                                                                                                             (4.12)

Эти колебания будут затухать в том и только в том случае, когда все отрицательны, и тогда движение будет устойчивым. Если же хотя бы одна из величин  окажется положительной, то движение будет иметь нарастающую во времени амплитуду колебаний и движение согласно определению будет неустойчивым.

Отсюда следует, что для устойчивости необходимо и достаточно, чтобы все корни алгебраического уравнения (4.10) имели отрицательные вещественные части. Поэтому, чтобы заранее знать, устойчива ли система или нет, нужно уметь, не решая уравнения (4.10), определять, будут ли вещественные части корней отрицательны или нет.

Признаки отрицательности вещественных частей всех корней алгебраического уравнения называются критериями Рауса−Гурвица. Не останавливаясь на доказательстве, приведем их для случаев уравнения с вещественными и с комплексными коэффициентами:

а) для того чтобы все корни алгебраического уравнения с вещественными коэффициентами

                                                                                                                                                                           (4.13)

имели отрицательные вещественные части, необходимо и достаточно, чтобы для матрицы n-го порядка

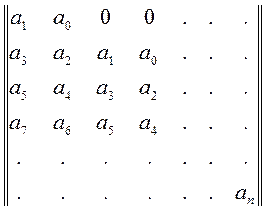
все главные миноры удовлетворяли условиям

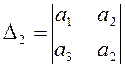>0, 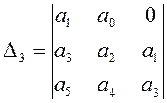  >0,

  > 0, … 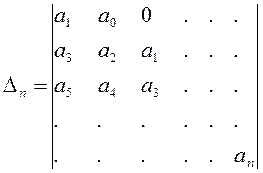> 0;                                                                                                                   (4.14)

б)  для того чтобы все корни алгебраического уравнения относительно р с комплексными коэффициентами имели отрицательную вещественную часть необходимо и достаточно, чтобы для преобразованного уравнения

 (4.15)

полученного из данного заменой р  на   jω, в   матрице  2 n-го порядка

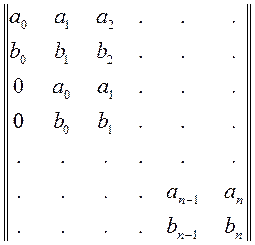
элемент а₀ и главные миноры четного порядка удовлетворяли условиям

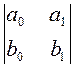> 0,   < 0, 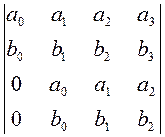 > 0.                                                                                                                   (4.16)

Если движение, определяемое однородной системой дифференциальных уравнений (4.9) устойчиво, то движение, определяемое системой (4.8) будет также устойчиво, если не имеет место случай, когда
Q_i = Q_0ie^jpkt, где p_k – комплексное число, равное одному из корней уравнения (4.10).

В качестве примера на применение критериев Рауса-Гурвица приведем определение условий устойчивости гибкого вала с  диском при действии внешнего и внутреннего трения. Движение описывается дифференциальным уравнениям изгибных колебаний вала при наличии дебаланса. Для уравновешенного вала имеем уравнение

                                                                                                                                                                             (4.17)