Устойчивость колебаний. Общая постановка и критерии устойчивости линейных систем. Специальные приемы исследования устойчивости, страница 3

Решение этого уравнения будет; после подстановки в уравнение (4.17) получим алгебраическое   уравнение относительно λ

На основании неравенств (4.16) имеем два условия устойчивости

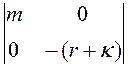< 0, 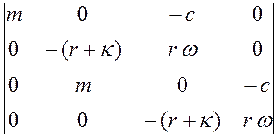> 0.                                                                                                                   (4.18)

Первое условие выполняется тождественно, а второе дает условие устойчивости вала

ω < ω₀ .

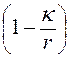Применение критериев Рауса-Гурвица при невысокой степени алгебраического уравнения частот еще возможно практически, однако при высокой степени уравнения и, в особенности при задании его коэффициентов не в численном, а в буквенном виде, использование этих критериев приводит к чрезвычайно большим вычислениям. Поэтому на практике для линейных систем применяются более эффективные приемы, позволяющие с помощью некоторой геометрической интерпретации судить об устойчивости заданной системы или построить для нее границу области устойчивости, зависящую от ее параметров. Условия устойчивости, получаемые на основании этих приемов, теоретически эквивалентны критериям Рауса-Гурвица, однако они получаются как бы „в обход“ последних, без необходимости делать большие вычисления.

4.2. Специальные приемы исследования устойчивости

Геометрический критерий устойчивости (критерий А.В. Михайлова). Для того чтобы определить, отрицательны ли вещественные части корней алгебраического уравнения (4.13), рассмотрим функцию

                                  (4.19)

Многочлен, стоящий в правой части (4.19), как известно из алгебры, можно   представить в   виде произведения, т. е.

                                    (4.20)

где     0р₁, р₂, …р_n – комплексные корни многочлена (4.19). Заменив р на jω, заставим величину ω пробегать все вещественные значения от –∞ до +∞. Тогда функция

                                                                                                                   (4.21)

на комплексной плоскости изобразится некоторой кривой. Определим приращение угла θ = argf(jω) при изменении  ω от –∞ до +∞. Так как аргумент произведения равен сумме аргументов сомножителей, то на основании (4.20) имеем

(4.22)

Но приращение каждого из выражений jω – p_kпри  изменении ω от
–∞ до +∞ будет   равно π, если p_kлежит в левой комплексной полуплоскости, и −π, если p_kлежит в правой полуплоскости. Иными словами, приращение аргумента будет ±π, причем знак + соответствует корням с отрицательной, − соответствует корням с положительной вещественной частью (рис. 4.1).

Заметим, что кривая (143) симметрична относительно вещественной оси, так какf(jω)  и  f(-jω) – комплексно-сопряженные числа, и
u(ω) = −u(ω). Поэтому можно рассматривать только ту часть кривой, которая соответствует изменению ω от 0 до +∞.

Обозначив число корней с отрицательной вещественной частью через l, а число корней с положительной вещественной частью через r, будем иметь

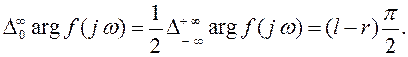                                                                                                                                                                              (4.23)

Отсюда видно, что при устойчивом движении, когда все корни имеют отрицательные вещественные части, l=n, r=0 и будет

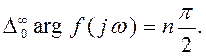                                                                                                                                                                             (4.24)

Легко видеть, что при устойчивом движении аргумент монотонно возрастает.

На основании формулы (4.24) можно сформулировать геометрический критерий устойчивости.

Для того, чтобы движение было устойчивым, необходимо и достаточно, чтобы кривая в комплексной плоскости, изображающая многочлен (4.19), при замене   р на  jω  при изменении ω  от 0 до ∞   последовательно   пересекала вещественную мнимую оси и имела всего п точек пересечения с осями, не проходя при этом через начало координат (проход через начало означает, что один из корней чисто мнимый). Соответствующая кривая показана на рис. 4.2.