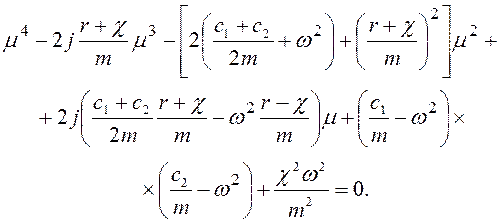Устойчивость колебаний. Общая постановка и критерии устойчивости линейных систем. Специальные приемы исследования устойчивости, страница 5

                                                                                                                                                                             (4.29)

Частоты собственных колебаний вала с достаточной точностью могут быть определены как для системы без трения, т.е. уравнения для χ = r = 0

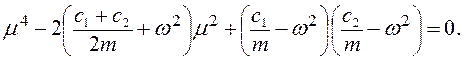                                                                                                                                                                             (4.30)

Зависимость между μ²  и  ω² показана графически на рис. 4.4, принято обозначение  и  .

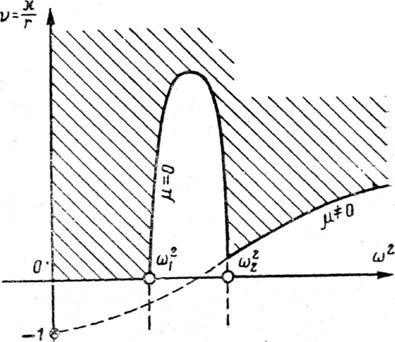
Построим области устойчивости и неустойчивости на основании уравнения (4.29), используя в качестве координат параметры − угловую скорость ω и отношение коэффициентов трения ν = χ/r. Эта граница соответствует вещественному значению корня уравнения (4.29). Полагая в уравнении (4.29) μ вещественными, отделим вещественную часть от мнимой в этом уравнении, что дает два алгебраических уравнения

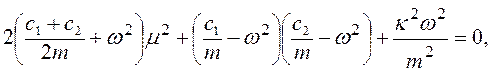                                                                                                                   (4.31)

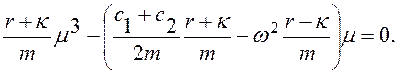                                                                                                                                                                             (4.32)

В формуле (4.31) опущено слагаемое 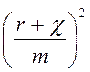 как имеющее второй порядок малости в сравнении с другим слагаемым в том же коэффициенте.

Таким образом, величина μ должна одновременно удовлетворять уравнениям (4.31) и (4.32). Определив μ² из (4.32) и вставив в(4.31), получим соотношение

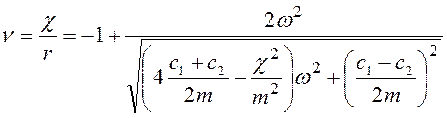.                                                                                                                                                                             (4.33)

Это соотношение связывает параметр ν = χ/r  с угловой скоростью ω на границе устойчивости при μ ≠ 0. Кроме того, есть решение μ = 0, которое может удовлетворять уравнениям (4.31) и (4.32) при условии, что выполняется соотношение

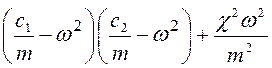< 0.

Это возможно только в том случае, когда ω лежит в интервале между с₁/т и с₂/т (см. рис. 4.4); в таком случае соотношение между ν и ω  определяется из уравнения

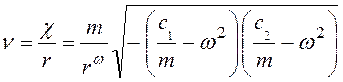.                                                                                                                                                                             (4.34)

Соотношение (4.33) и соотношение (4.34) являются двумя ветвями границы устойчивости в плоскости параметров ν и  ω. Изображение этих кривых дано на рис. 4.5.

Остается выяснить с какой стороны от границы, определяемой этими  соотношениями расположена область устойчивости.

Как уже указывалось, область устойчивости располагается слева от границы, если двигаться вдоль границы в сторону встающих значений μ. Если обратиться к рис. 4.4, то видно, что в области, начиная от некоторой средней точки между  и  , величина μ растет с увеличением ω, поэтому на кривой рис. 4.5 увеличению ω соответствует рост μ, а это значит, что область устойчивости расположена вверху.

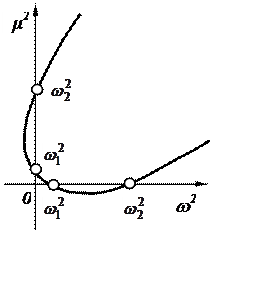Область  устойчивости

Область устойчивости на рис. 4.5 заштрихована.

БИБЛИОГРАФИЧЕСКИЙ  СПИСОк 

1. Артоболевский И.И. теория механизмов и машин. – М.: Наука, 1975.с – 640 с.

2. Бабаков И.М. Теория колебаний. – 2 изд. – М.: Наука, 1965.
– 559 с.

3. Бердников В.В. Основы теории машин авиационной техники: Учебное пособие для студентов втузов / Казанский авиационный ин-т. – Казань, 1981. – 92 с.

4. Бидерман В.А. Теория механических колебаний. – М.: Высшая школа, 1980. – 408 с.

5. Бихман И.И. Синхронизация в природе и технике.  – М.: Наука, 1981. – 352 с.

6. Вейц В.Л. Динамика машинных агрегатов. – Л.: Машиностроение, 1969. – 368 с.