Методические указания к практическим занятиям по дисциплине "Высшая математика". Часть 2. Задачи для самостоятельного решения по теории вероятностей

Оглавление:

Элементы математического анализа ………………………………………… 3

Элементы теории вероятностей …………………………………………….. 40

Задачи для самостоятельного решения по мат. анализу ……………….. 56

Задачи для самостоятельного решения по теории вероятностей ….…. 66

Список литературы

Бугров Я. С., Никольский С. М. Дифференциальное и интегральное исчисление. М., Наука, 1988.

Вентцель Е. С. Теория вероятностей. М., Наука, 1998.

Коваленко И. Н., Филиппова А. А. Теория вероятностей и математическая статистика. М., Высшая школа, 1982.

Кудрявцев Л. Д. Краткий курс математического анализа. т. 1,2. Альфа, 1998.

2

Вариант 10.

1. На собрании должно выступить 5 человек: А, Б, В, Г, Д. Сколькими способами можно расположить их в списке ораторов при условии, что В не должен выступать до того, как выступит А? Если В должен выступать сразу после А?

2. Вынимают две косточки домино.

Событие А – на одной из вынутых косточек "три-пусто"

Событие В – сумма очков на одной из вынутых косточек равна трем

Событие С – сумма очков на вынутых косточках меньше шести.

Дать описание событий  А&В,  А+В,  &В,  ,  С&А,  С+В.

3. Из колоды, состоящей из 36 карт, вынимают пять карт. Найти вероятности следующих событий

- среди этих карт хотя бы один туз

- ровно три карты черные

- хотя бы три карты одной масти.

4. Три студента сдают экзамен. Вероятность того, что первый студент сдаст экзамен равна 0,85. Для второго студента эта вероятность – 0,9, для третьего – 0,7. Найти вероятности следующих событий:

- все трое не сдали экзамен

- хотя бы один сдал экзамен

- экзамен сдали двое.

5. Вся продукция проверяется двумя контролерами. Вероятность того, что изделие попадет на проверку к первому контролеру 0,6, а ко второму – 0,4. Вероятность того, что первый пропустит нестандартное изделие 0,01, а второй – 0,02. Взятое наудачу изделие с маркой "стандарт" оказалось бракованным. Найти вероятность того, что оно проверялось вторым контролером.

6. Вероятность успеха в одном эксперименте равна 0,75. Эксперимент проводится 6 раз. Найти вероятность того, что

- ровно пять результатов успешны

- хотя бы пять результатов успешны

- ровно два результата неудачны.

7. В колоде 36 карт. Наудачу вынимают три карты. Случайная величина Х – количество пик среди вынутых. Построить ряд распределения для случайной величины Х, найти математическое ожидание, дисперсию и функцию распределения случайной величины.

8. Плотность распределения случайной величины Х .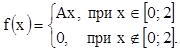

Найти А, М(Х), D(Х), F(х), P(X<0,5). Р(Х>1,1).

9. Найти вероятность того, что при 300 бросаниях монеты герб выпадает менее 130 раз.

10. Случайная величина подчиняется нормальному закону распределения с математическим ожиданием m=8 и дисперсией 3. Найти вероятность того, что случайная величина

- отрицательна

- находится в промежутке от 3 до 6.

11. По схеме Бернулли было проведено 8 опытов, и из них в двух произошло событие А. Найдите с надежностью g=0,7 доверительный интервал для вероятности события А.

12. Контрольные обмеры двадцати валиков дали следующие результаты: 7,39;  7,43;  7,54;  7,64;  7,40;  7,55;  7,40;  7,26;  7,42;  7,50;  7,32;  7,31;  7,28;  7,52;  7,46;  7,63;  7,38;  7,44;  7,52;  7,53. Дать точечные оценки для размера валика и его дисперсии.

75

Следует запомнить следующие стандартные символы:

º - равно (ставится между множествами),

" - любой,

$ - существует,

: - такой, что (такая, что и т.п.)

АºВ означает, что множества А и В состоят из одних и тех же элементов.

Из АºВ следует, что АÌВ и ВÌА.

Примеры использования:

"  а Î А читается: любой элемент множества А;

$ а Î А – существует элемент а, принадлежащий множеству А.

Действия с множествами:

¨ Пересечение множеств.

Пересечением множеств А и В называется множество, состоящее из элементов, принадлежащих обеим множествам (т.е. пересечение – общая часть А и В). Пересечение А.и В обозначается А·В, А&В, АÙВ, АÇВ. Эти обозначения тождественны. Пересечение множеств иногда называют произведением множеств.

Примеры:

1. А – множество всех равнобедренных треугольников;

    В - множество всех прямоугольных треугольников

    (А·В) – множество всех прямоугольников с равными катетами.

2. А – множество всех брюнеток;

    В – множество всех голубоглазых женщин;

    (А·В) – множество всех брюнеток с голубыми глазами.

¨ Объединение множеств.

Объединением двух множеств А и В называется множество, состоящее из всех элементов, входящих хотя бы в одно из них. Объединение множеств А и В обозначается А+В, АÚВ, АÈВ. Объединение множеств иногда называют суммой множеств.

Примеры:

1. А – множество всех людей ростом выше 2 м. 10 см.;

    В – множество всех людей ростом ниже 1 м. 45 см.;

    (А+В) – множество всех людей нестандартного роста.

¨ Разность множеств.

Разностью множеств А и В называется множество, состоящее из тех элементов множества А, которые не входят в множество В. Разность множеств А и В обозначается А\В. А-В.

Примеры:

1. А – множество всех брюнеток;

    В – множество всех голубоглазых женщин;

    А\В – множество брюнеток с любым, кроме голубого, цветом глаз;