Методические указания к практическим занятиям по дисциплине "Высшая математика". Часть 2. Задачи для самостоятельного решения по теории вероятностей, страница 11

               Если закон распределния случайной величины задан рядом или плотностью распределния, математическое ожидание и дисперсия рассчитываются по следующим формулам:

для дискретной случайной величины:

;             

для непрерывной случайной величины:

;          

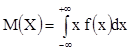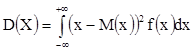
Часто, задавая закон распределения случайной величины, дискретной или непрерывной, используют функцию распределения .

Тогда .

Из определения функции распределения F(х) следуют ее свойства:

1)

2) ,

47

...	...

4. Используем формулу (5), принимая n=7 и учитывая, что (х- х₀)=0,25

»

 Погрешность D при этом равна , где (×)с Î (1; 1,25), , D>0.

Получен следующий результат:

Î(1,05737033; 1,05737145),

Î(2,11474066; 2,11474290).

Ответ: приближенное значение с пятью верными знаками после запятой: »2,11474. (для сравнения: значение  с девятью верными знаками после запятой, вычисленное калькулятором по аналогичной формуле с большим числом слагаемых =2,114742527... .)

1.8 Интеграл.

1.8.1 Первообразная и неопределенный интеграл

               Первообразной функции f(х) называется функция F(х), для которой выполнено равенство

.                                                     (1)

Доказано, что для функции f(х), имеющей первообразную F(х), функция F(х)+С, где С – любое число, также будет первообразной, и других первообразных f(х) иметь не будет. Множество всех первообразных функции f(х) принято называть неопределенным интегралом и обозначать . Из этого следует:

32

Ряд распределения примет вид:

               Непрерывной случайной величиной называют такую случайную величину, множество значений которой полностью заполняет один или несколько промежутков на числовой оси. Примерами непрерывной случайной величины могут служить рост прохожего, время ожидания трамвая, температура воздуха и т.п.

               Закон распределения непрерывной случайной величины задают в виде плотности распределения. Плотностью распределения непрерывной случайной величины называют функцию f(x), обладающую следующим свойством:

Р(а£Х<b)=.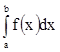

Это означает, что вероятность для случайной величины Х попасть в промежуток от а до b равна, площади, ограниченной вертикальными

прямыми x=a, x=b, ось ОХ и графиком функции у= f(x).

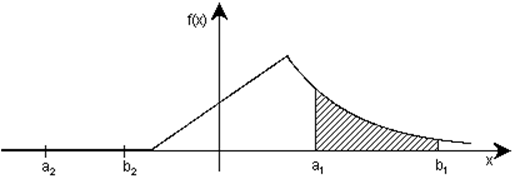
Если график плотности распределения имеет вид, изображенный на рисунке, то Р(а₁£Х<b₁)=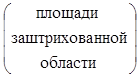, Р(а₂£Х<b₂)=0.

               Плотность распределения f(х) для любой случайной величины Х обладает следующими свойствами:

1) f(х)³0 (кривая плотности не может лежать ниже оси ОХ)

2)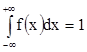 (площадь, ограниченная осью ОХ и графиком f(х) равна 1).

Если на промежутке [a, b] f(x)=0, то Р(а£Х<b)=0.

Непрерывная случайная величина обладает одним интересным свойством: Р(Х=а)=0 для любого а, т.е. каждое ее значение имеет

45

что для некоторых функций f(х) с увеличением n, при более или менее равномерном дроблении промежутка [a,b] на части значения интегральных сумм будут приближаться к некоторому числу S, т.е. существует предел последовательности интегральных сумм при n®¥

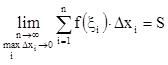                                        (4)

и этот предел не зависит от способа дробления [a,b] на части и выбора точек x_i внутри каждой части.

               Число S, определенное равенством (4), называют определенным интегралом f(х) от а до b, и обозначают .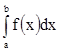

Из сказанного выше следует:

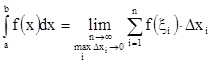,                           (5)

если данный предел существует.

               Функции, для которых существует предел последовательности интегральных сумм, называют интегрируемыми. Достаточным условием интегрируемости f(х) является ее непрерывность на [a,b].

Часто интегральную сумму функции f(х) на [a,b], равную  называют интегральной суммой определенного интеграла 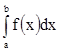 и говорят, что определенный интеграл – это предел последовательности интегральных сумм при n®¥.