- все шесть результатов успешны
- хотя бы один результат неудачен
- ровно один результат успешен
7. В ящике 6 белых и 3 синих шарика, одинаковых на ощупь. Наудачу вынимают четыре шара. Случайная величина Х – количество синих шаров среди вынутых. Построить ряд распределения для случайной величины Х, найти математическое ожидание, дисперсию и функцию распределения случайной величины.
8. Плотность распределения случайной величины
Х 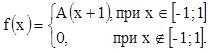 .
.
Найти А, М(Х), D(Х), F(х), P(X<0,5). Р(Х>2).
9. Найти вероятность того, что при 800 бросаниях монеты герб выпадает не более 350 раз.
10. Случайная величина подчиняется нормальному закону распределения с математическим ожиданием m=10 и дисперсией 3. Найти вероятность того, что случайная величина
- будет больше 14
- отклонится от математического ожидания не более чем на 5.
11. По схеме Бернулли было проведено 9 опытов, и из них в трех произошло событие А. Найдите с надежностью g=0,9 доверительный интервал для вероятности события А.
12. Контрольные обмеры диаметров болтов дали следующие результаты: 2,31; 2,28; 2,29; 2,28; 2,32; 2,28; 2,32; 2,29; 2,31; 2,32.
Найти точечные оценки для диаметра болта и его дисперсии в контролируемом процессе производства.
68
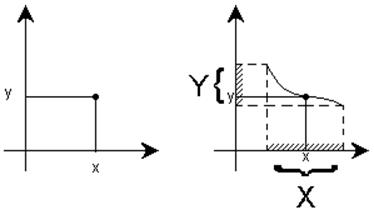
- графический, при котором приводится график функции; значения y=f(х) при различных х при этом снимаются с графика.
При аналитическом способе задания легко построить график функции; при графическом способе задания перейти к аналитическому иногда легко, иногда трудно, иногда невозможно.
Приведем примеры функций, заданных аналитически:
f(х)=х2; f(х)=sin(2x+10); f(х)=![]()
Отметим следующее: если функция задана аналитически, ее значения при различных х получаются подстановкой соответствующего значения х в формулу.
Напрмер: f(х)=![]() (или у(х)=
(или у(х)= ![]() ).
).
Тогда ![]()
![]()
![]()
![]()
![]()
![]() и т.п.
и т.п.
1.5 Предел функции.
Понятие предела пронизывает весь математический анализ, да и в других областях математики играет важную роль. Установление
9
Вариант 5.
1. В магазине 15 сортов пирожных. Каким количеством способов можно выбрать 5 разных? Каким количеством способов можно выбрать 5 пирожных, не обязательно разных?
2. Из колоды карт вынимают четыре карты.
Событие А – три из них красные.
Событие В – все карты черные.
Событие С – среди этих карт нет пик.
Дать описание событий А&В, А+В, ![]() &В,
&В, ![]() ,
С&А, С+В.
,
С&А, С+В.
3. Из колоды, состоящей из 36 карт, вынимают три карты. Найти вероятности следующих событий:
- среди этих карт хотя бы один туз
- все три карты черные
- все три карты одной масти.
4. Три станка работают независимо друг от друга. Вероятность того, что первый станок проработает смену без наладки 0,8, второй – 0,9, а третий – 0,95. Найти вероятности следующих событий:
- ровно один станок проработает смену без наладки
- все станки потребуют наладку
- хотя бы один станок потребует наладку.
5. Вся продукция проверяется двумя контролерами. Вероятность того, что изделие попадет на проверку к первому контролеру 0,6, а ко второму – 0,4. Вероятность того, что первый пропустит нестандартное изделие 0,01, а второй – 0,02. Взятое наудачу изделие с маркой "стандарт" оказалось бракованным. Найти вероятность того, что оно проверялось вторым контролером.
6 Вероятность успеха в одном эксперименте равна 0,3. Эксперимент проводится 12 раз. Найти вероятность того, что
- все двенадцать результатов неудачны
- хотя бы один результат успешен
- ровно восемь результатов неудачны
7. В ящике 5 белых и 5 синих шариков, одинаковых на ощупь. Наудачу вынимают три шара. Случайная величина Х – количество синих шаров среди вынутых. Построить ряд распределения для случайной величины Х, найти математическое ожидание, дисперсию и функцию распределения случайной величины.
8. Плотность распределения случайной величины
Х 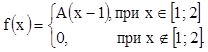 .
.
Найти А, М(Х), D(Х), F(х), P(X<0,5). Р(Х>1,2).
9. Найти вероятность того, что при 400 бросаниях монеты герб выпадает не более 180 раз.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.