9. Цены на товар три раза повышались на 5%. На сколько процентов возросла цена по сравнению с первоначальной? На сколько процентов надо уменьшить достигнутую цену, чтобы она стала равна первоначальной?
10. Банк выплачивает клиентам 14% годового дохода. Какой процент годового дохода можно получить, ежемесячно снимая проценты и добавляя их к вкладу? До какой максимальной величины можно довести процент годового дохода? Все операции проводятся бесплатно.
58
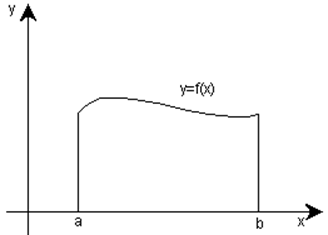
Точку х0 называют точкой разрыва функции у= f(х) в двух случаях:
во-первых, если х0ÏХ, но является точкой сгущения Х, или
во-вторых, если х0ÎХ, но ![]() .
.
Если точка х0 не является точкой сгущения Х, то вопрос о непрерывности или разрыве функции f(х) в этой точке вообще не рассматривается.
Пример 1.
Исследовать непрерывность функции f(х)=![]() .
.
Решение: областью определения функции
является вся числовая ось, кроме точки х=0, Х º (-¥;0) È (0;+¥).
В любой точке х0¹0
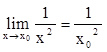 , следовательно функция непрерывна во всех
точках своей области определения.
, следовательно функция непрерывна во всех
точках своей области определения.
Точка х0=0 является точкой
сгущения Х, но х0ÏХ,
и следовательно х0=0 является точкой разрыва функции f(х)=![]() .
.
Пример 2.
Исследовать непрерывность функции f(х)=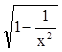 .
.
Решение:
Областью определения функции является множество Х º (-¥; -1) È (1;+¥).
При всех других значениях аргумента подкоренное выражение, входящее в функцию, становится отрицательным, и корень из него не существует.
19
Вариант 5.
1. Построить один из возможных вариантов
графика функции у=f(х),
для которой ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
2. Вычислить
![]() ,
, ![]() ,
, ![]() ,
,
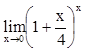 ,
, 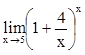 ,
, 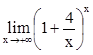 .
.
3. Найти точки разрыва, асимптоты, интервалы
монотонности и экстремумы функций ![]() ,
, ![]() . Построить графики функций.
. Построить графики функций.
4. Вычислить приближенно ![]() , используя пять слагаемых в формуле
Тейлора. Сравнить с точным значением.
, используя пять слагаемых в формуле
Тейлора. Сравнить с точным значением.
5. Вычислить по формуле Ньютона-Лейбница 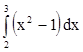 ,
, 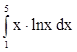 .
.
6. Составить любую интегральную сумму при n=4 для интеграла 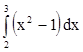 . Сравнить ее значение с точным значением
интеграла.
. Сравнить ее значение с точным значением
интеграла.
7. Найти ![]() в
произвольной точке и точке М0 (1,4,-2), если
в
произвольной точке и точке М0 (1,4,-2), если ![]() .
.
8. Найти экстремумы функции ![]() .
.
9. Цены на товар три раза повышались на 4%. На сколько процентов возросла цена по сравнению с первоначальной? На сколько процентов надо уменьшить достигнутую цену, чтобы она стала равна первоначальной?
10. Банк выплачивает клиентам 12% годового дохода. Какой процент годового дохода можно получить, ежемесячно снимая проценты и добавляя их к вкладу? До какой максимальной величины можно довести процент годового дохода? Все операции проводятся бесплатно.
60
Довольно часто раскрытие неопределенностей сводится к одному из двух пределов, которые называются
первый замечательный предел
![]()
и второй замечательный предел
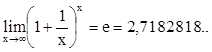 .
.
В первом случае раскрыта одна из
неопределенностей вида ![]() , во втором - [1¥]. В любом учебнике по
математическому анализу приводится подробный вывод этих результатов.
, во втором - [1¥]. В любом учебнике по
математическому анализу приводится подробный вывод этих результатов.
Следует заметить, что и в первом и во втором замечательных пределах вместо х может стоять любое выражение, главное, чтобы это выражение стремилось к нулю в первом замечательном пределе, и к бесконечности во втором замечательном пределе. Проиллюстрируем это:
1) ![]() , т.к. 2х ® 0 при х ®
0, аргумент синуса и знаменатель совпадают;
, т.к. 2х ® 0 при х ®
0, аргумент синуса и знаменатель совпадают;
2) ![]() , т.к. (p-х) ®
0 при х ® p, аргумент синуса и знаменатель совпадают;
, т.к. (p-х) ®
0 при х ® p, аргумент синуса и знаменатель совпадают;
3) ![]() не является первым
замечательным пределом, так как аргумент синуса не совпадает знаменателем, но
этот предел можно привести к первому замечательному пределу, умножив на 7
числитель и знаменатель:
не является первым
замечательным пределом, так как аргумент синуса не совпадает знаменателем, но
этот предел можно привести к первому замечательному пределу, умножив на 7
числитель и знаменатель: ![]() , т.к.
, т.к. ![]() , 7х ®
0 при х ® 0.
, 7х ®
0 при х ® 0.
4) ![]() не является первым
замечательным пределом, т.к. аргумент синуса и знаменатель не стремятся к нулю;
не является первым
замечательным пределом, т.к. аргумент синуса и знаменатель не стремятся к нулю;
![]() . Этот предел не содержит неопределенности.
. Этот предел не содержит неопределенности.
17
Вариант 7.
1. Построить один из возможных вариантов
графика функции у=f(х),
для которой ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
2. Вычислить
![]() ,
, ![]() ,
, ![]() ,
,
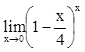 ,
, 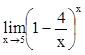 ,
, 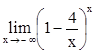 .
.
3. Найти точки разрыва, асимптоты, интервалы
монотонности и экстремумы функций ![]() ,
, ![]() . Построить графики функций.
. Построить графики функций.
4. Вычислить приближенно ![]() , используя пять слагаемых в формуле
Тейлора. Сравнить с точным значением.
, используя пять слагаемых в формуле
Тейлора. Сравнить с точным значением.
5. Вычислить по формуле Ньютона-Лейбница 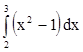 ,
, 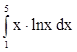 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.