Методические указания к практическим занятиям по дисциплине "Высшая математика". Часть 2. Задачи для самостоятельного решения по теории вероятностей, страница 7

3.  - это неопределенность, для ее раскрытия проведем следующее алгебраическое преобразование: поделим числитель и знаменатель на х:

.

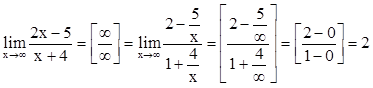16

Вариант 6.

1. Построить один из возможных вариантов графика функции у=f(х), для которой , , , .

2. Вычислить

, , ,

, , .

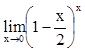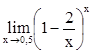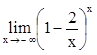3. Найти точки разрыва, асимптоты, интервалы монотонности и экстремумы функций , . Построить графики функций.

4. Вычислить приближенно , используя пять слагаемых в формуле Тейлора. Сравнить с точным значением.

5. Вычислить по формуле Ньютона-Лейбница , .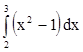

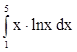6. Составить любую интегральную сумму при n=4 для интегра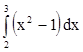ла . Сравнить ее значение с точным значением интеграла.

7. Найти  в произвольной точке и точке М₀ (1,4,-2), если .

8. Найти экстремумы функции .

9. Цены на товар три раза повышались на 4%. На сколько процентов возросла цена по сравнению с первоначальной? На сколько процентов надо уменьшить достигнутую цену, чтобы она стала равна первоначальной?

10. Банк выплачивает клиентам 12% годового дохода. Какой процент годового дохода можно получить, ежемесячно снимая проценты и добавляя их к вкладу? До какой максимальной величины можно довести процент годового дохода? Все операции проводятся бесплатно.

61

5)  можно свести ко второму замечательному пределу заменой . При a®0 очевидно, что ®¥. .

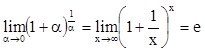6) 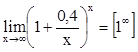 - приводится ко второму замечательному пределу заменой , х = 0,4t, t ® ¥ при х ® ¥; .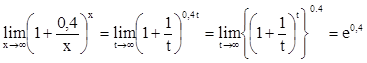

7) 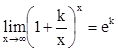 приводится ко второму замечательному пределу заменой .

1.6 Непрерывность функции.

Рассмотрим функцию f(х) определенную на множестве Х, и пусть точка х₀ÎХ, так что f(х₀) принимает определенное значение. Если при этом

,                                                 (1)

то говорят, что f(х) непрерывна в точке х₀, или точка х₀ есть точка непрерывности функции у= f(х).

               Функция f(х) называется непрерывной на промежутке (а;b), если она непрерывна в любой точке этого промежутка. График функции, непрерывной на (а;b), представляет собой непрерывную линию.

18

Вариант 4.

1. Построить один из возможных вариантов графика функции у=f(х), для которой , , , .

2. Вычислить

, , ,

, , .

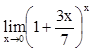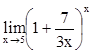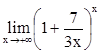3. Найти точки разрыва, асимптоты, интервалы монотонности и экстремумы функций , . Построить графики функций.

4. Вычислить приближенно , используя пять слагаемых в формуле Тейлора. Сравнить с точным значением.

5. Вычислить по формуле Ньютона-Лейбница , .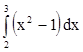

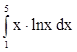6. Составить любую интегральную сумму при n=4 для интегра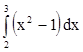ла . Сравнить ее значение с точным значением интеграла.

7. Найти  в произвольной точке и точке М₀ (1,4,-2), если .

8. Найти экстремумы функции .

9. Цены на товар три раза повышались на 4%. На сколько процентов возросла цена по сравнению с первоначальной? На сколько процентов надо уменьшить достигнутую цену, чтобы она стала равна первоначальной?

10. Банк выплачивает клиентам 12% годового дохода. Какой процент годового дохода можно получить, ежемесячно снимая проценты и добавляя их к вкладу? До какой максимальной величины можно довести процент годового дохода? Все операции проводятся бесплатно.

59

В любой точке х₀ÎХ 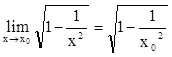, следовательно функция непрерывна во всех точках своей области определения. Точки из промежутка (-1; 1) не являются точками разрыва или точками непрерывности, так как ни одна из этих точек не является точкой сгущения множества Х. Точки промежутка (-1; 1) – это просто точки, не входящие в область определения функции.

               Рассмотрим классификацию точек разрыва.

Если х₀ – точка разрыва функции f(х) и пределы  и  существуют и конечны, то точку х₀ называют точкой разрыва первого рода или говорят, что в точке х₀ функция у= f(х) терпит разрыв первого рода.

               Если х₀ – точка разрыва первого рода, но существует конечный предел , то точку х₀ называют точкой устранимого разрыва первого рода, так как потребовав, чтобы х₀ÎХ и f(х₀)=, мы сделаем точку х₀ точкой непрерывности.

               Если х₀ – точка разрыва функции у=f(х) и хотя бы один из пределов,  или , не существует или равен бесконечности, то точку х₀ называют точкой разрыва второго рода.