1. Лингвисту попадает текст, написанный при помощи 26 незнакомых знаков. Эти знаки – буквы, каждая из которых обозначает один из 26 звуков. Сколькими способами можно сопоставить звуки знакам текста?
2. Из колоды карт вынимают четыре карты.
Событие А – все карты одной масти.
Событие В – все карты - пики
Событие С – среди этих карт ровно один туз.
Дать описание событий А&В, А+В, ![]() &В,
&В, ![]() ,
С&А, С+В.
,
С&А, С+В.
3. В футбольном первенстве принимают участие 14 команд. Две команды, занявшие последние места, покидают лигу. При отсутствии какой-либо информации о подготовке команд, найти вероятности угадать:
- кто покинет лигу
- кто войдет в тройку призеров
- кто займет первое и второе места, а кто покинет лигу.
4. Три стрелка стреляют по мишени. Вероятность попадания первого стрелка равна 0.7, второго - 0.9, третьего - 0.85. Найти вероятности следующих событий:
- промахнулся хотя бы один стрелок.
- попал ровно один стрелок.
- попал хотя бы один стрелок
- все трое промахнулись.
5. Среди партии деталей 40% окрашенных. Вероятность того, что окрашенная деталь тяжелее нормы, равна 0,3. Для неокрашенной детали эта вероятность равна 0,1. Взятая наудачу деталь оказалась тяжелее нормы. Найти вероятность того, что она окрашена.
6. Вероятность успеха в одном эксперименте равна 0,8. Эксперимент проводится 6 раз. Найти вероятность того, что
- все шесть результатов неудачны
- хотя бы одна неудача
- ровно пять успехов.
7. В ящике 8 белых и 2 синих шарика, одинаковых на ощупь. Наудачу вынимают три шара. Случайная величина Х – количество белых шаров среди вынутых. Построить ряд распределения для случайной величины Х, найти математическое ожидание, дисперсию и функцию распределения случайной величины.
8. Плотность распределения случайной величины
Х 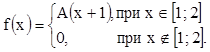 .
.
Найти А, М(Х), D(Х), F(х), P(X<0,5). Р(Х>1,2).
9. Найти вероятность того, что при 500 бросаниях монеты герб выпадает не менее 280 раз.
10. Случайная величина подчиняется нормальному закону распределения с математическим ожиданием m=5 и дисперсией 10. Найти вероятность того, что случайная величина
- положительна
- отклонится от математического ожидания не более чем на 5.
11. По схеме Бернулли было проведено 8 опытов, и из них в четырех произошло событие А. Найдите с надежностью g=0,85 доверительный интервал для вероятности события А.
12. Контрольные обмеры двадцати валиков дали следующие результаты: 7,39; 7,43; 7,54; 7,64; 7,40; 7,55; 7,40; 7,26; 7,42; 7,50; 7,32; 7,31; 7,28; 7,52; 7,46; 7,63; 7,38; 7,44; 7,52; 7,53. Дать точечные оценки для размера валика и его дисперсии.
71
ния функции. Если "yÎY соответствует какому-нибудь хÎХ, то Y называют областью изменения y=f(x). Следует еще раз подчеркнуть, что Х – произвольное множество, Y – числовое множество. Любой элемент хÎХ называют аргументом f(x), y=f(x) называют значением функции, соответствующим аргументу х.
Примеры функции:
1. Х – множество сотрудников ГМТУ;
х – какой-либо студент;
y=f(x) – числовое выражение роста студента х, измеряемого в указанных единицах (футах, метрах или сантиметрах).
(если y=f(x) не рост, который соответственно измеряется числом, а, например, цвет глаз, то y=f(x) не будет функцией, если только заранее каждому возможному оттенку глаз не поставить в соответствие свой номер-число)
2. Х – множество звезд на небе;
х – какая-то звезда;
y=f(x) – числовое выражение массы этой звезды.
3. Х – множество вещественных чисел.
Y=х2.
Замечание: если Y не является числовым множеством, закон соответствия между хÎХ и yÎY называют оператором, а не функцией.
1.4 Функция числового аргумента.
Функции, у которых и область изменения Y, и область определения Х являются числовыми множествами, то есть подмножествами R, называют функциями вещественной переменной.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.