Приведем два примера составления интегральных сумм.
Пример 1.
Составить интегральную сумму для 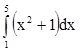 при n=6.
при n=6.
Решение:
- разбиваем промежуток [1, 5] на шесть частей произвольным образом
![]()
- находим Dх1=1, Dх2=0,5, Dх3=0,5, Dх4=0,8, Dх5=0,6, Dх6=0,6 (проверяем: 1+0,5+0,5+0,8+0,6+0,6=5-1)
- выбираем x1=1,2, x2=2,4, x3=2,7, x4=3,5, x5=4, x6=4,5
34
Решение:
1) 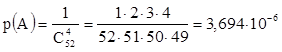
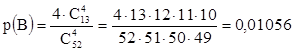
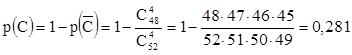
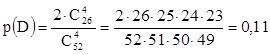
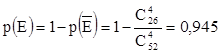
2) А×В=Æ, р(А×В)=0
АС=А, р(АС)=3,694×10-6
А+С=С, р(А+С)=0,281
![]() - все карты красные, р(
- все карты красные, р(![]() )=
)=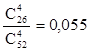
![]() ×В – вынуты или 4 червы, или 4 бубны р(
×В – вынуты или 4 червы, или 4 бубны р(![]() ×В)=
×В)=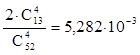
![]() ×Е – нет тузов, но есть хотя бы одна черная
карта, р(
×Е – нет тузов, но есть хотя бы одна черная
карта, р(![]() ×Е)
×Е)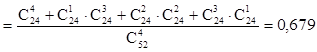
Для вычисления вероятности р(![]() ×Е)
событие
×Е)
событие ![]() ×Е
было представлено в виде суммы несовместных событий:
×Е
было представлено в виде суммы несовместных событий:
S4 – среди четырех карт нет тузов и все четыре карты черные;
S3 – среди четырех карт нет тузов и среди них три черных и одна красная;
S2 – среди четырех карт нет тузов и среди них две черных и две красных;
S1 – среди четырех карт нет тузов и среди них одна черная и три красных.
р(S4)=![]() ; р(S3)=
; р(S3)=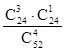 ; р(S2)=
; р(S2)=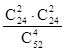 ;
р(S1)=
;
р(S1)=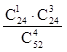 .
.
43
f(x2)= |
f(x4)= |
- составляем интегральную сумму ![]() 0,3076923×0,5+
0,3076923×0,5+
+0,2666666×0,5+0,2352941×0,5+0,2105263×0,5=0,5100898…
2. n=20
- проводим действия, аналогичные действиям первого пункта: Dх1=Dх2=…=Dх20=0,1; x1=-1,95, x2=-1,55, …, x2=-0,05
![]() 0,0510796002…
0,0510796002…
3. n=40
Dх1=Dх2=…=Dх40=0,05; x1=-1,975, x2=-1,925, …, x2=-0,025
![]() 0,510818216…
0,510818216…
Ответ: ![]() =0,5100898…
=0,5100898…
![]() =0,0510796002…
=0,0510796002…
![]() =0,510818216…
=0,510818216…
Сравним полученные значения интегральных сумм в примере 2.
![]() отличается от
отличается от ![]() на величину D@0,0007,
на величину D@0,0007,
![]() отличается от
отличается от ![]() примерно
на 0,00002. Можем считать, что
примерно
на 0,00002. Можем считать, что 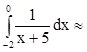 0,5108, причем
погрешность в ответе меньше, чем 0,0001, что видно при сравнении
0,5108, причем
погрешность в ответе меньше, чем 0,0001, что видно при сравнении ![]() и
и ![]() .
.
Заметим, что любой определенный интеграл 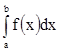 легко вычислить с желаемой степенью
точности, составив для него интегральную сумму с достаточно большим значением n. Мы не будем здесь
останавливаться подробно на различных схемах, применяемых при вычислении
определенных интегралов. Принципиальная основа этих схем уже показана.
легко вычислить с желаемой степенью
точности, составив для него интегральную сумму с достаточно большим значением n. Мы не будем здесь
останавливаться подробно на различных схемах, применяемых при вычислении
определенных интегралов. Принципиальная основа этих схем уже показана.
Очевидно, что такие методы
нахождения значения 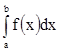 являются слишком трудоемкими.
Поэтому классический метод вычисления интеграла
являются слишком трудоемкими.
Поэтому классический метод вычисления интеграла 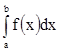 ,
предложенный более двухсот
,
предложенный более двухсот
36
Любое его подмножество назовем событием, а вероятность события равна сумме вероятностей элементарных событий, это событие образующих.
Например:
А º {w1, w3} - событие, его вероятность р(А)=р1+р3
В º {w5} - тоже событие, р(В)=р5
С º W называют достоверным событием, р(W)=1
Æ (пустое множество) – невозможное событие, р(Æ)=0.
Отсюда:
Теорема 1.
р(А+В)=р(А)+р(В)-р(АВ)
Теорема 2.
р(А×В)=р(А)×р(В/А).
р(В/А) означает вероятность события А при условии, что событие В произошло.
Теорема 3.
р(![]() )=1-р(А).
)=1-р(А).
![]() обозначает событие,
противоположное событию А, т.е. все, кроме А.
обозначает событие,
противоположное событию А, т.е. все, кроме А.
Если А×ВºÆ, то события А и В называются несовместными. Для
несовместных событий р(А+В)=р(А)+р(В).
Если р(А)=р(А/В) и р(В)=р(В/А), то события А и В называются независимыми. Для независимых событий р(АВ)=р(А)×р(В).
2.2 Классическая вероятность.
Если в вероятностном
пространстве р1=р2= ... =рn=![]() , то схему вероятностного пространства
называют классической и вероятность события А Ì W рассчитывается по
формуле
, то схему вероятностного пространства
называют классической и вероятность события А Ì W рассчитывается по
формуле
![]() ,
,
где ![]() -
количество элементарных исходов, входящих в А.
-
количество элементарных исходов, входящих в А.
Число ![]() называют
количеством благоприятных для А исходов.
называют
количеством благоприятных для А исходов.
![]() .
.
Пример 1.
В урне 5 белых и 3 черных шарика. Наугад вынимают один шарик. Найти вероятность того, что вынутый шар - черный.
Решение:
n=8 (возможных элементарных исходов здесь восемь, т.к. шариков в урне восемь, и вынимая один шарик мы вынимаем любой из восьми);
41
Пример 2.
Вычислить 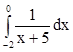
Решение:
- найдем ![]()
- 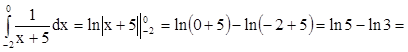 0,510825623…
0,510825623…
Ответ: 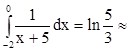 0,510825623…
0,510825623…
Сравнивая точное значение интеграла с его интегральной
суммой ![]() 0,510818216…, видим, что разность между
ними составляет 0,001%, т.е.
0,510818216…, видим, что разность между
ними составляет 0,001%, т.е. ![]() и точное значение
практически совпадают.
и точное значение
практически совпадают.
Из (5) и (6) легко получить свойства определенного интеграла:
1) 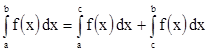
2) 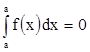
3) 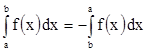
4) если a<b и f(х)³0, то 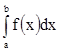 ³0
³0
5) если на интервале [a, b] все значения функции у=f(х) лежат между m и М, то есть m£ f(х)£М "хÎ[a, b], то существует число mÎ[m, М], такое что
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.