Предел 
называют
правосторонним и обозначают 
.
Предел 
называют
левосторонним и обозначают 
.
Определение предела (*) для односторонних пределов меняется.
означает, что
" 
$ 
: х Î Ç Х Þ
f(х) Î . (**)
означает, что
12
Вариант 10.
1. Построить один из возможных вариантов
графика функции у=f(х),
для которой 
, 
, 
, 
.
2. Вычислить
, 
, 
,
, 
, 
.
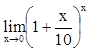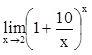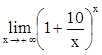3. Найти точки разрыва, асимптоты, интервалы
монотонности и экстремумы функций 
, 
. Построить графики функций.
4. Вычислить приближенно 
, используя пять слагаемых в формуле
Тейлора. Сравнить с точным значением.
5. Вычислить по формуле Ньютона-Лейбница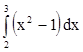 
, 
.
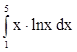6. Составить любую интегральную сумму при n=4 для интегра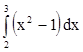ла . Сравнить ее значение с точным значением
интеграла.
7. Найти 
в
произвольной точке и точке М0 (1,4,-2), если 
.
8. Найти экстремумы функции 
.
9. Цены на товар три раза повышались на 4%. На сколько процентов возросла цена по сравнению с первоначальной? На сколько процентов надо уменьшить достигнутую цену, чтобы она стала равна первоначальной?
10. Банк выплачивает клиентам 12% годового дохода. Какой процент годового дохода можно получить, ежемесячно снимая проценты и добавляя их к вкладу? До какой максимальной величины можно довести процент годового дохода? Все операции проводятся бесплатно.
65
заданной аналитически, пользуются теоремами о пределах и информацией о пределах
элементарных функций.
Теоремы о пределах:
Теорема 1.
]
=А, a
- конечное постоянное число.
Тогда 
=aА (постоянный множитель выносится за знак
предела).
Замечание: если А=¥, то =
.
Теорема 2.
]
=А, 
=В.
Тогда 
=А+В
(предел суммы равен сумме пределов).
Замечания: 1) если А=¥, В – конечное число, то =
;
2) если А=+¥, В=+¥
(или А= -¥, В= -¥), то =
(или 
);
3) теорема 2 на работает, если А=+¥, В= - ¥.
Теорема 3.
]
=А, =В.
Тогда 
=А×В (предел произведения равен произведению
пределов).
Замечания: 1) если А=¥, В¹0,
то 
;
2) теорема 3 не работает, если А=0, В=¥.
Теорема 4.
]
=А, =В.
Тогда 
.
(предел частного равен частному пределов).
Замечания: 1) если А¹0; В=0, то 
;
2) если А¹¥;
В=¥, то 
;
3) теорема 4 не работает, если А=0, В=0 или А=¥, В=¥.
14
Вариант 8.
1. Построить один из возможных вариантов
графика функции у=f(х),
для которой 
, 
, 
, 
.
2. Вычислить
, 
, 
,
, 
, 
.
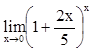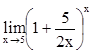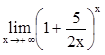3. Найти точки разрыва, асимптоты, интервалы
монотонности и экстремумы функций , . Построить графики функций.
4. Вычислить приближенно , используя пять слагаемых в формуле
Тейлора. Сравнить с точным значением.
5. Вычислить по формуле Ньютона-Лейбница , .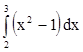
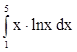6. Составить любую интегральную сумму при n=4 для интегра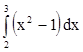ла . Сравнить ее значение с точным значением
интеграла.
7. Найти в
произвольной точке и точке М0 (1,4,-2), если .
8. Найти экстремумы функции 
.
9. Цены на товар три раза повышались на 4%. На сколько процентов возросла цена по сравнению с первоначальной? На сколько процентов надо уменьшить достигнутую цену, чтобы она стала равна первоначальной?
10. Банк выплачивает клиентам 12% годового дохода. Какой процент годового дохода можно получить, ежемесячно снимая проценты и добавляя их к вкладу? До какой максимальной величины можно довести процент годового дохода? Все операции проводятся бесплатно.
63
ответ также получается сразу. Перечислим еще раз варианты, предусмотренные замечаниями:
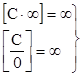(здесь С=const¹0)
(здесь С=const¹¥)
,
(здесь С=const¹¥)
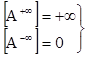(здесь А=const>1)
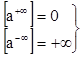(здесь а=const Î (0;1)).
Если в результате подстановки получают неопределенность, ответ не может быть назван сразу, для его получения требуются некоторые преобразования, иногда простые, иногда довольно сложные.
Каждый конкретный пример, представляющий собой неопределенность, имеет свой конкретный ответ, который может оказаться любым числом.
Приведем примеры вычисления пределов, не содержащих неопределенность или содержащих ее.
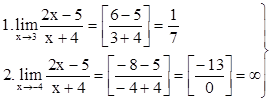пределы не содержат
неопределенности, ответ получен сразу, без дополнительных преобразований.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.