2. Из колоды карт вынимают три карты.
Событие А – все карты красные.
Событие В – все карты черные.
Событие С – среди этих карт нет тузов.
Дать описание событий А&В, А+В, ![]() &В,
&В, ![]() ,
С&А, С+В.
,
С&А, С+В.
3. В забеге участвуют семь лошадей. Найти вероятность того, что при отсутствии какой-либо информации о них Вы угадаете, кто из лошадей
- попадет в первую тройку
- займет первое, второе и третье места
- будет последней.
4. Три стрелка стреляют по мишени. Вероятность попадания первого стрелка равна 0.8, второго - 0.9, третьего - 0.75. Найти вероятности следующих событий:
- попал хотя бы один стрелок.
- попал ровно один стрелок.
- попали ровно два стрелка.
- все трое промахнулись.
5. Среди партии деталей 40% окрашенных. Вероятность того, что окрашенная деталь тяжелее нормы, равна 0,3. Для неокрашенной детали эта вероятность равна 0,1. Взятая наудачу деталь оказалась тяжелее нормы. Найти вероятность того, что она окрашена.
6. Вероятность успеха в одном эксперименте равна 0,9. Эксперимент проводится 8 раз. Найти вероятность того, что
- все восемь результатов успешны
- хотя бы один результат неудачен
- ровно один результат неудачен
7. В ящике 5 белых и 3 синих шарика, одинаковых на ощупь. Наудачу вынимают четыре шара. Случайная величина Х – количество синих шаров среди вынутых. Построить ряд распределения для случайной величины Х, найти математическое ожидание, дисперсию и функцию распределения случайной величины.
8. Плотность распределения случайной величины
Х 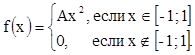 .
.
Найти А, М(Х), D(Х), F(х), P(X<0,5). Р(Х>2).
9. Найти вероятность того, что при 400 бросаниях монеты герб выпадает не более 170 раз.
10. Случайная величина подчиняется нормальному закону распределения с математическим ожиданием m=3 и дисперсией 0,25. Найти вероятность того, что случайная величина
- будет больше своего математического ожидания
- отклонится от математического ожидания более чем на единицу.
11. По схеме Бернулли было проведено 9 опытов, и из них в трех произошло событие А. Найдите с надежностью g=0,8 доверительный интервал для вероятности события А.
12. Контрольные обмеры диаметров болтов дали следующие результаты: 2,31; 2,28; 2,29; 2,28; 2,32; 2,28; 2,32; 2,29; 2,31; 2,32.
Найти точечные оценки для диаметра болта и его дисперсии в контролируемом процессе производства.
66
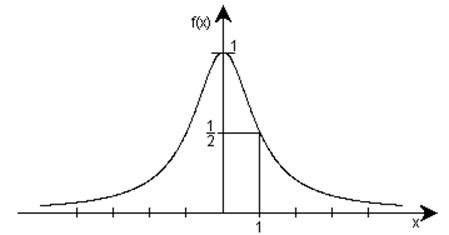
Рис. 1
Из вида графика следует, что, например, ![]() ,
, ![]() ,
, ![]() .
.
На рисунке 2 изображен график функции f(х)=х3-х2-х+4.
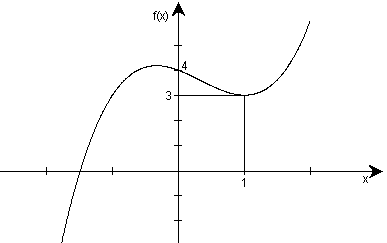
Рис. 2
Из вида графика следует, что ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Можно рассмотреть и другие варианты.
Из вида графика функции y=f(х), изображенного на
рисунке 3, видно, что ![]() ,
, ![]() .
.
11
Вариант 3.
1. В магазине 12 сортов пирожных. Каким количеством способов можно выбрать 5 разных? Каким количеством способов можно выбрать 5 пирожных, не обязательно разных?
2. В урне черные, белые и синие шары. Вынимают четыре шара.
Событие А – все шары белые.
Событие В – все шары одного цвета.
Событие С – среди этих шаров хотя бы один синий.
Дать описание событий А&В, А+В, ![]() &В,
&В, ![]() ,
С&А, С+В.
,
С&А, С+В.
3. В забеге участвуют восемь лошадей. Найти вероятность того, что при отсутствии какой-либо информации о них Вы угадаете, кто из лошадей
- попадет в первую тройку
- кто займет второе и третье места
- кто будет предпоследним.
4. Три стрелка стреляют по мишени. Вероятность попадания первого стрелка равна 0.8, второго - 0.9, третьего - 0.75. Найти вероятности следующих событий:
- попал хотя бы один стрелок.
- попал ровно один стрелок.
- попали ровно два стрелка.
- все трое промахнулись.
5. Изделие может поступить для обработки на первый станок с вероятностью 0,2, на второй с вероятностью 0,3 и на третий – с вероятностью 0,5. При обработке на первом станке вероятность брака 0,02, на втором – 0,03, на третьем 0,1. Выбранное наудачу изделие оказалось бракованным. Найти вероятность того, что оно обрабатывалось на втором станке.
6. Вероятность успеха в одном эксперименте равна 0,7. Эксперимент проводится 6 раз. Найти вероятность того, что
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.