Если Х1, Х2,
…, Хn – независимые случайные величины, имеющие одно и то же
распределение с математическим ожиданием m и дисперсией s2, то при увеличении n закон распределения
суммы ![]() неограниченно приближается к нормальному с
математическим ожиданием
неограниченно приближается к нормальному с
математическим ожиданием ![]() и
и ![]() (
(![]() ).
).
Пример:
Монету бросают 700 раз. Найти вероятность того, что количество выпаданий герба будет заключено в промежутке от 330 до 370.
Решение:
Рассмотрим случайную величину Хi – количество выпадений герба при
одном, i-том броске. Ряд распределения Xi для любого i:
|
Хi |
0 |
1 |
|
Р |
|
|
М(Хi)=m=0×![]() +1×
+1×![]() =
=![]()
D(Хi)= s2=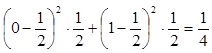
![]()
Количество выпадений
герба ![]() распределено нормально с
распределено нормально с
54
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. 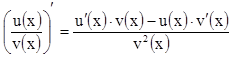
6. ![]()
В последнем правиле, которое называется
правило дифференцирования сложной функции, ![]() -
производная функции F(u)
по аргументу u.
-
производная функции F(u)
по аргументу u.
Теперь приведем таблицу производных элементарных функций, и рядом с производной каждой элементарной функции покажем, что изменится (согласно правилу 6), если аргументом элементарной функции в свою очередь будет какая-то функция от х.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23
Вариант 1.
1. Построить один из возможных вариантов
графика функции у=f(х),
для которой ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
2. Вычислить
![]() ,
, ![]() ,
, ![]() ,
,
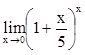 ,
, 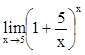 ,
, 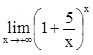 .
.
3. Найти точки разрыва, асимптоты, интервалы
монотонности и экстремумы функций ![]() ,
, ![]() . Построить графики функций.
. Построить графики функций.
4. Вычислить приближенно ![]() , используя пять слагаемых в формуле
Тейлора. Сравнить с точным значением.
, используя пять слагаемых в формуле
Тейлора. Сравнить с точным значением.
5. Вычислить по формуле Ньютона-Лейбница 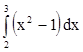 ,
, 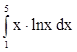 .
.
6. Составить любую интегральную сумму при n=4 для интеграла 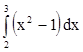 . Сравнить ее значение с точным значением
интеграла.
. Сравнить ее значение с точным значением
интеграла.
7. Найти ![]() в
произвольной точке и точке М0 (1,4,-2), если
в
произвольной точке и точке М0 (1,4,-2), если ![]() .
.
8. Найти экстремумы функции ![]() .
.
9. Цены на товар три раза повышались на 4%. На сколько процентов возросла цена по сравнению с первоначальной? На сколько процентов надо уменьшить достигнутую цену, чтобы она стала равна первоначальной?
10. Банк выплачивает клиентам 12% годового дохода. Какой процент годового дохода можно получить, ежемесячно снимая проценты и добавляя их к вкладу? До какой максимальной величины можно довести процент годового дохода? Все операции проводятся бесплатно.
56
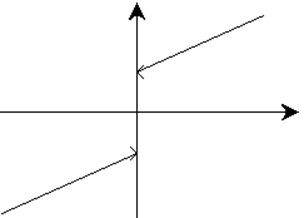
Неустранимый разрыв первого рода (скачок) в точке х0=0.
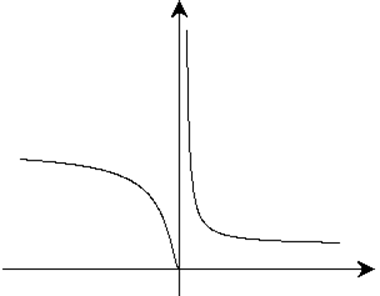
Разрыв второго рода в точке х0=0.
Часто используется определение функции, непрерывной в точке в точке х0 в другой форме. Введем предварительно понятие приращения функции f(х) в точке в точке х0.
Приращением функции f(х) в точке в точке х0 называется разность между значениями функции в точках (х0+Dх) и х0. Приращение f(х) обозначается Df(х).
Df(х0)=f(х0+Dх)- f(х0). (2)
Например:
при f(х)=![]()
21
Вариант 3.
1. Построить один из возможных вариантов
графика функции у=f(х),
для которой ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
2. Вычислить
![]() ,
, ![]() ,
, ![]() ,
,
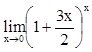 ,
, 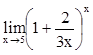 ,
, 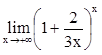 .
.
3. Найти точки разрыва, асимптоты, интервалы
монотонности и экстремумы функций ![]() ,
, ![]() . Построить графики функций.
. Построить графики функций.
4. Вычислить приближенно ![]() , используя пять слагаемых в формуле
Тейлора. Сравнить с точным значением.
, используя пять слагаемых в формуле
Тейлора. Сравнить с точным значением.
5. Вычислить по формуле Ньютона-Лейбница 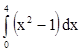 ,
, 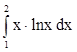 .
.
6. Составить любую интегральную сумму при n=4 для интеграла 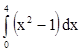 . Сравнить ее значение с точным значением
интеграла.
. Сравнить ее значение с точным значением
интеграла.
7. Найти ![]() в
произвольной точке и точке М0 (0,1,-2), если
в
произвольной точке и точке М0 (0,1,-2), если ![]() .
.
8. Найти экстремумы функции ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.