Методические указания к практическим занятиям по дисциплине "Высшая математика". Часть 2. Задачи для самостоятельного решения по теории вероятностей, страница 16

а) Р(1<Х<1,2)=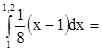0,0025

б) Р(2,5<Х<2,7)=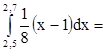0,04

в) Р(4,8<Х<5)=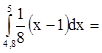0,0975.

Можно сделать вывод, что для значения данной случайной величины более вероятно попадание в окрестность пяти, чем в окрестность 2,5, а тем более, единицы.

Ряд распределения или функция распределения случайной величины полностью описывают поведение случайной величины и дают

46

4. Используем формулу (5), приняв n=9 и учитывая, что (х- х₀)=0,2

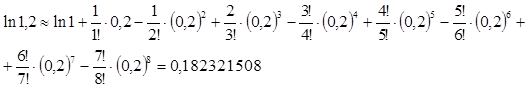
Погрешность D при этом равна , где (×)с Î (1; 1,2), 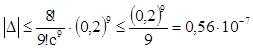, D>0.

Получен следующий результат:

ln1,2Î(0,182321508; 0,182321508+D),

ln1,2Î(0,182321508; 0,182321564).

Ответ: приближенное значение ln1,2 с семью верными знаками после запятой: ln1,2»0,1823215. (для сравнения: значение логарифма с девятью верными знаками после запятой ln1,2=0,182321556.)

Замечание: любой калькулятор или компьютер при вычислении ln1,2 использует тот же алгоритм с достаточно большим n.

Пример 2.

Вычислить значение  с точностью до пяти знаков после запятой.

Решение:

Преобразуем , учитывая, что ближайшее число, из которого корень четвертой степени известен, равно 16: =2, 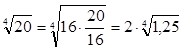. Будем искать .

1. Рассмотрим функцию .

2. Выберем х₀=1, х=1,25.

3. Найдем производные первого, второго и т.д. порядков от функции  и вычислим их значения в точке х₀=1.

31

3) если х₁<х₂, то F(х₁) £ F(х₂)

4) F(х) непрерывна слева, т.е.

Из определения также следует:

- если F(х) непрерывна в точке х=с, то Р(Х=с)=0

- если F(х)=const на (c, d), то Р(c<X<d)=0

- если Х непрерывная случайная величина, то F(х) непрерывна и , где f(х) – плотность распределения

- если Х дискретная случайная величина и Р(Х=с)=р, то в точке х=с функция распределения имеет разрыв, "скачок", величина которого равна р.

Используя два последних утверждения, всегда можно, зная F(х), получить ряд распределения или плотность распределения случайной величины.

Если, например, F(х) имеет вид, изображенный на рисунке,

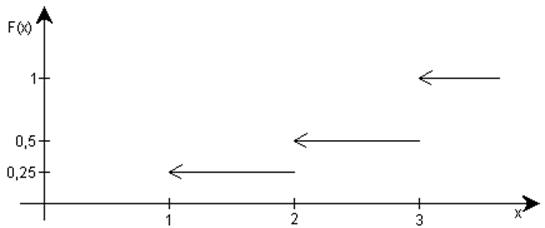
то очевидно: случайная величина дискретна и ее ряд распределения имеет следующий вид:

М(Х)=1×0,25+2×0,25+3×0,5=2,25

D(Х)=(1-2,25)²×0,25+(2-2,25)²×0,25+(3-2,25)²×0,5=0,688

0,829.

Если, например,

48

         

         

          

           .

               Приведем некоторые формулы для производных n-ого порядка.

                        

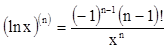
               Можно было бы привести здесь формулы для производных n-ого порядка и других элементарных функций, но на самом деле производные высших порядков гораздо легче находить, непосредственно вычисляя первую, вторую и т.д. производные конкретной функции, пользуясь на каждом шаге правилами и формулами, изложенными в разделе, посвященном производным первого порядка.

1.7.4 Формула Тейлора.

               Рассмотрим произвольную функцию y=f(х), определенную на множестве Х и имеющую на этом множестве производные всех порядков до n-ого включительно.

               Зафиксирует точку х₀ÎХ и составим многочлен

29

.

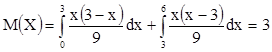
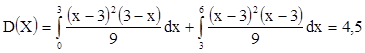
               Рассмотрим три классических типа распределения дискретной случайной величины.

2.3.1 Биномиальное распределение.

Пусть производится n независимых опытов, результатом каждого опыта является или успех (событие А), или неудача (событие ).

Р(А)=р=const в любом опыте (0<p<1)

P()=1-p=q

Случайной величиной в серии из n опытов назовем Х – число успехов в серии. Очевидно, Х принимает значения {0; 1; 2; …; n-1; n}. Легко показать, что Р(Х=m)=, математическое ожидание M(X)=np, дисперия D(X)=npq, .

Пример 1:

Передается 5 сообщений по каналу связи. Каждое сообщение искажается с вероятностью р=0,3 независимо от других искажений. Случайная величина Х – количество искаженных сообщений. Построить

ряд распределения этой случайной величины, найти M(X)=m_x и D(X)=.

Решение:

р=0,3, q=1-0,3=0,7

Х	0	1	2	3	4	5
Р