6. Вероятность успеха в одном эксперименте равна 0,4. Эксперимент проводится 8 раз. Найти вероятность того, что
- хотя бы шесть результатов будут успешны
- хотя бы один результат будет успешным
- ровно один результат будет успешным
7. В ящике 3 белых и 5 синих шариков, одинаковых на ощупь. Наудачу вынимают четыре шара. Случайная величина Х – количество белых шаров среди вынутых. Построить ряд распределения для случайной величины Х, найти математическое ожидание, дисперсию и функцию распределения случайной величины.
8. Плотность распределения случайной величины
Х 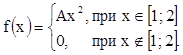 .
.
Найти А, М(Х), D(Х), F(х), P(X<0,5). Р(Х>1,1).
9. Найти вероятность того, что при 900 бросаниях монеты герб выпадает не более 350 раз.
10. Случайная величина подчиняется нормальному закону распределения с математическим ожиданием m=11 и дисперсией 169. Найти вероятность того, что случайная величина
- будет отрицательной
- отклонится от математического ожидания не более чем на 26.
11. По схеме Бернулли было проведено 10 опытов, и из них в четырех произошло событие А. Найдите с надежностью g=0,8 доверительный интервал для вероятности события А.
12. Контрольные обмеры диаметров болтов дали следующие результаты: 2,31; 2,28; 2,29; 2,28; 2,32; 2,28; 2,32; 2,29; 2,31; 2,32.
Найти точечные оценки для диаметра болта и его дисперсии в контролируемом процессе производства.
74
1. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА.
1.1 Множества. Действия с множествами.
Понятие множества, как и некоторые другие понятия в математике, не определяется. Любая попытка дать определение множества становится злоупотреблением словарным богатством русского языка. Для того, чтобы определить какое-либо понятие, нужно прежде всего указать, частным случаем какого более общего понятия оно является. Для понятия множества сделать это невозможно, так как более общего понятия, чем множество, в математике нет. Георг Кантор подчеркнул это следующими словами: "Множество есть многое, мыслимое нами как единое."
Любое множество вводится описанием. Например: множество слонов в зоопарке; множество всех целых положительных чисел; множество стульев в здании института.
Особо выделяют множество, не содержащее ни одного объекта, так называемое пустое множество.
Объекты, образующие множество, называются его элементами.
Как правило, множество обозначается одной из заглавных букв латинского алфавита (А, В, М и.т.п.), а его элементы соответствующими строчными буквами с индексами или без (а1, b15, m и т.п.).
За некоторыми множествами закреплены стандартные обозначения:
Æ - пустое множество (не содержащее ни одного элемента);
N – множество всех целых неотрицательных чисел;
Z – множество всех целых чисел;
R – множество всех действительных чисел.
Запись аÎА означает следующее: а является одним из элементов, образующих множество А, или, что то же самое, а принадлежит множеству А;
аÏА означает, что элемент а не принадлежит А.
Кроме символа Î (принадлежит) используется еще один символ принадлежности: Ì, который ставят только между двумя множествами.
АÌВ означает, что множество А является частью множества В (т.е. если какой-либо элемент принадлежит А, то он обязательно принадлежит и В) и В называют подмножеством А.
Например, N есть подмножество Z, NÌZ. Также NÌR; ZÌR.
Считается, что запись ÆÌА верна для любого множества А, т.е. пустое множество является подмножеством любого множества.
Для удобства действий с множествами вводят понятие универсального множества, т.е. множества, содержащего любые элементы и включающего в себя любое множество. Обычно универсальное множество обозначают I. АÌI верно для любого А.
3
Арцыкова Н.А.
Методические указания к практическим занятиям
по высшей математике
для специальности "экономика"
часть 2
СПбГМТУ
Кафедра математики
2001
Санкт-Петербург
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.