7. В ящике 3 белых и 5 синих шариков, одинаковых на ощупь. Наудачу вынимают три шара. Случайная величина Х – количество белых шаров среди вынутых. Построить ряд распределения для случайной величины Х, найти математическое ожидание, дисперсию и функцию распределения случайной величины.
8. Плотность распределения случайной величины
Х 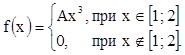 .
.
Найти А, М(Х), D(Х), F(х), P(X<0,5). Р(Х>1,4).
9. Найти вероятность того, что при 900 бросаниях монеты герб выпадает не менее 500 раз.
10. Случайная величина подчиняется нормальному закону распределения с математическим ожиданием m=1 и дисперсией 3. Найти вероятность того, что случайная величина
- будет положительной
- отклонится от математического ожидания не более чем на 5.
11. По схеме Бернулли было проведено 11 опытов, и из них в четырех произошло событие А. Найдите с надежностью g=0,9 доверительный интервал для вероятности события А.
12. Контрольные обмеры диаметров болтов дали следующие результаты: 2,31; 2,28; 2,29; 2,28; 2,32; 2,28; 2,32; 2,29; 2,31; 2,32.
Найти точечные оценки для диаметра болта и его дисперсии в контролируемом процессе производства.
72
2. А – множество всех целых чисел;
В – множество всех четных чисел;
А\В – множество всех нечетных чисел;
В\А – пустое множество.
Если В является частью А (ВÌ А), то разность А\В называют дополнением В до А.
¨ Разбиение множеств.
Пусть множество А является суммой (пересечением) своих подмножеств, никакие два из которых не имеют общих элементов, т.е. выполнено два условия:
АºВ1+В2+В3+ ... +Вn;
Вi·BjºÆ, если i¹j.
Тогда В1,В2,В3, ..., Вn называют разбиением множества А на n подмножеств (или типов, или видов, или классов и т.п.).
Примеры:
1. При составлении каталога в библиотеке все множество книг разбивается на подмножества, в каждом из которых фамилии авторов начинаются на одну и ту же букву.
2. Все целые числа разбивается на две группы – четные числа и нечетные числа.
1.2 Числовое множество. Окрестность точки.
Точка сгущения числового множества.
Числовым множеством называют любое подмножество множества R. Каждому элементу этого множества (числу) ставят в соответствие точку на числовой оси. Соответствие это взаимно-однозначное: после того, как на прямой, которую называют числовой осью, отмечают две точки, соответствующий числам "0" и "1" (причем точка, соответствующая числу "0", находится левее точки, соответствующей числу "1"), каждой точке на прямой соответствует одно и только одно число, (т.е. каждому числу соответствует одна точка и разным числам - разные точки). Множеству R соответствует вся числовая ось, множеству [a; b] соответствует отрезок от точки х=а до точки х=b, множеству [1;+¥) – луч от точки х=1 вправо и т.п.

Окрестностью радиуса r конечной точки а называется множество (a-r;a+r).
![]()
5
Вариант
9.
1. Имеется семь монет достоинством 1 копейка, 5 копеек, 10 копеек, 50 копеек, 1 рубль, 2 рубля, 5 рублей. Каким количеством способов можно разложить эти монеты по двум карманам?
2. Вынимают косточку домино.
Событие А – на вынутой косточке "три-пусто"
Событие В – сумма очков на вынутой косточке равна трем
Событие С – сумма очков на вынутой косточке равна шести.
Дать описание событий А&В, А+В, ![]() &В,
&В, ![]() ,
С&А, С+В.
,
С&А, С+В.
3. В забеге участвуют восемь лошадей. Найти вероятность того, что при отсутствии какой-либо информации о них Вы угадаете, кто из лошадей
- попадет в первую тройку
- займет первое и второе места
- будет последним.
4. Три студента сдают экзамен. Вероятность того, что первый студент сдаст экзамен равна 0,85. Для второго студента эта вероятность – 0,9, для третьего – 0,7. Найти вероятности следующих событий:
- все трое сдали экзамен
- хотя бы один не сдал экзамен
- экзамен сдали двое.
5. В спартакиаде участвуют: из первой группы 4 студента, из второй – 6, из третьей – 5. Студент первой группы попадает в сборную института с вероятностью 0,9, из второй – с вероятностью 0,7, из третьей – с вероятностью 0,8. Студент попал в сборную. Найти вероятность того, что студент учится в третьей группе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.