Несколько примеров вычисления производных с использованием правил дифференцирования и таблицы производных:
1) 
(по (1*),
n=1)
2) 
(по
(1*), n=12)
3) 
(исп. правила 2 и
3, а также (1*))
4) 
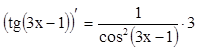(по (8**), u(х)=3х-1)
5) 
(по (7**), n=3, u(х)=х3+4х-1)
6) 
(по (1**), n=3, u(х)=cosx)
7) 
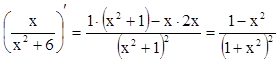(правила 5 и 2,
формула (1*)).
1.7.2 Использование производных при исследовании
поведения функции.
Определение 1.
Функция y=f(х) называется
убывающей на <a,b>, если меньшему
значению аргумента соответствует большее значение функции: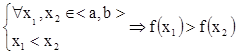 
.
Определение 2.
Функция y=f(х) называется
возрастающей на <a,b>, если большему значению аргумента
соответствует большее значение функции: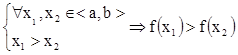 
.
Определение 3.
Функция y=f(х) называется монотонной на <a,b>, если она или убывает или возрастает на <a,b>.
24
, 
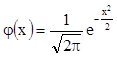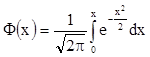(F(0)=0; F(-х)=-F(х);
F(+¥)=
)
.
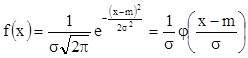
Для такой случайной
величины с параметрами (m,
s) 
.
Нормальный закон распределения в теории вероятностей занимает среди других особое положение. По нормальному закону или закону, близкому к нормальному, распределяются ошибки измерений, а также множество других "ошибок", сопровождающих нормальную деятельность человека.
Пример:
Измерительный прибор имеет положительную систематическую ошибку 5 мм и среднюю квадратическую ощибку 7,5 мм. Какова вероятность того, что ошибка измерения
1) будет положительной (т.е. измерение дает результаты больше истинного)
2) будет отрицательной
3) не превзойдет по абсолютной величине 5 мм.
Решение:
Х -ошибка измерения, распределна по нормальному закону с m=5 мм, s=7,5 мм. Тогда
1) 
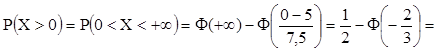
0,7475
(значение F(0,6666) берем из таблиц)
2) 
0,2525
3) 
=
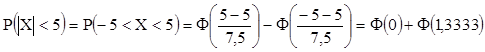=0+0,4087=0,4087.
Нормальное распределение возникает также в тех случаях, когда случайная величина Х является суммой независимых или слабо зависимых случайных величин Х1, Х2, …, Хn или их средним
53
y=f(х) имеет производную
и возрастает на <a,b> Û 
³ 0 " х Î <a,b>.
Теорема 2.
В точках экстремума производная функции равна нулю или не существует (необходимый признак существования экстремума).
(×)
х0 – точка экстремума функции y=f(х) Þ 
=0 или
не существует.
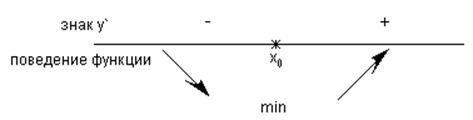
Теорема 3.
Если функция имеет производную и в некоторой проколотой окрестности точки х0 производная функции равна нулю или не существует и при переходе через эту точку производная функции меняет знак, то в этой точке функция имеет экстремум (достаточный признак существования экстремума).
1) =0 или
не существует, ö
2) $
такая что "х Î 
< 0 ý Þ
в (×)х0 у=f(х) имеет min
"х Î
> 0 ø
1) =0 или
не существует, ö
2) $
такая что "х Î > 0 ý Þ
в (×)х0 у=f(х) имеет max
"х Î
< 0 ø
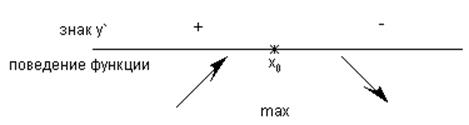
Используя теоремы 1-3, можно исследовать поведение различных функций и находить их экстремальные значения.
Пример 1.
Исследовать
функцию 
; указать ее интервалы монотонности, найти
экстремальные значения, построить график.
Решение:
1) функция определена на всей числовой оси
26
0,055
2.3.2 Распределение Пуассона.
Говорят, что случайная величина Х
распределена по закону Пауссона, если она может принимать все возможные целые
неотрицательные значения: {0; 1; 2; …; m; m+1; …} и Р(Х=m)=
. Для этого распределения М(Х)=а, D(Х)=а.
Распределение Пуассона является предельным для биномиального, когда число опытов неограниченно увеличивается (n®¥), а вероятность успеха в каждом опыте неограниченно уменьшается, но так, что n×p=а (произведение n×p сохраняет постоянное значение).
Пример:
Пусть вероятность успеха в одном опыте р=0,001. Проводится 2000 опытов. Найти вероятность того, что
1) ни один опыт не будет успешным (Х=0)
2) хотя бы один опыт будет успешным (Х³1)
3) успешных опытов будет ровно два (Х=2)
4) количество успехов будет больше двух (Х³3).
Решение:
Случайная величина Х (количество успехов) распределена по биномиальному закону, но так как n=2000 и nр=2 (n достаточно велико, р
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.