В\А – множество всех голубоглазых женщин, но не брюнеток.
4
Вариант 8.
1. Каким количеством способов из 25 человек, входящих в научное общество, можно выбрать президента, вице-президента, ученого секретаря и казначея, если один человек может занимать не более чем два поста?
2. Из колоды карт вынимают четыре карты.
Событие А – две из них красные.
Событие В – все карты красные.
Событие С – среди этих карт нет пик.
Дать описание событий А&В, А+В, 
&В, 
,
С&А, С+В.
3. Участники игры зачеркивают на игровой карте 5 чисел из 25. Во время розыгрыша объявляют пять выигравших номеров. Найти вероятность для игрока
- не угадать не более двух номеров
- угадать хотя бы три числа
- угадать ровно три числа.
4. Три станка работают независимо друг от друга. Вероятность того, что первый станок проработает смену без наладки 0,85, второй – 0,95, а третий – 0,9. Найти вероятности следующих событий:
- все станки проработают смену без наладки
- все станки потребуют наладку
- хотя бы один станок проработает смену без наладки
- ровно два станка проработают смену без наладки.
5. Изделие может поступить для обработки на первый станок с вероятностью 0,2, на второй с вероятностью 0,3 и на третий – с вероятностью 0,5. При обработке на первом станке вероятность брака 0,02, на втором – 0,03, на третьем 0,1. Выбранное наудачу изделие оказалось бракованным. Найти вероятность того, что оно обрабатывалось на втором станке.
6. Вероятность успеха в одном эксперименте равна 0,85. Эксперимент проводится 7 раз. Найти вероятность того, что
- ровно пять результатов успешны
- хотя бы пять результатов успешны
- ровно один результат неудачен.
7. В ящике 8 белых и 2 синих шарика, одинаковых на ощупь. Наудачу вынимают три шара. Случайная величина Х – количество синих шаров среди вынутых. Построить ряд распределения для случайной величины Х, найти математическое ожидание, дисперсию и функцию распределения случайной величины.
8. Плотность распределения случайной величины
Х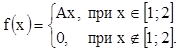 
.
Найти А, М(Х), D(Х), F(х), P(X<0,5). Р(Х>1,4).
9. Найти вероятность того, что при 200 бросаниях монеты герб выпадает менее 80 раз.
10. Случайная величина подчиняется нормальному закону распределения с математическим ожиданием m=5 и дисперсией 2. Найти вероятность того, что случайная величина
- отрицательна
- находится в промежутке от 3 до 6.
11. По схеме Бернулли было проведено 9 опытов, и из них в двух произошло событие А. Найдите с надежностью g=0,8 доверительный интервал для вероятности события А.
12. Контрольные обмеры двадцати валиков дали следующие результаты: 7,39; 7,43; 7,54; 7,64; 7,40; 7,55; 7,40; 7,26; 7,42; 7,50; 7,32; 7,31; 7,28; 7,52; 7,46; 7,63; 7,38; 7,44; 7,52; 7,53. Дать точечные оценки для размера валика и его дисперсии.
73
Окрестность радиуса r конечной точки а
обозначается 
. Если хÎ, то х удовлетворяет неравенству
или –r < x-a < r, или a-r < x
< a+r.
Если r1<r2, то 
. При этом говорят, что окрестность 
более узкая, чем окрестность 
. Для того, чтобы сузить окрестность
конечной точки, надо уменьшить радиус окрестности.
Правой окрестностью радиуса r конечной точки а
называется множество (a;a+r), которое обозначается 
.
Если хÎ, то х удовлетворяет
неравенству
0 < x-a < r или a < x < a+r.
Левой окрестностью радиуса r конечной точки а
называется множество (a-r;a) которое обозначается 
.
Если хÎ, то х удовлетворяет
неравенству
-r < x-a < 0 или a-r < x < a.
Проколотой окрестностью
радиуса r
конечной
точки а называется объединение правой и левой окрестностей этой точки È, обозначается 
.
Если хÎ, то х удовлетворяет
неравенству
.
Проколотая окрестность не содержит точки а.
Множество (- ¥; -R) È (R;+ ¥) называется окрестностью радиуса R бесконечно удаленной
точки (или окрестностью точки ¥)
и обозначается 
.
Если хÎ, то х удовлетворяет
неравенству
6
Вариант 6.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.