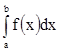Методические указания к практическим занятиям по дисциплине "Высшая математика". Часть 2. Задачи для самостоятельного решения по теории вероятностей, страница 13

=m×(b-a).                                                    (7)

Это число m=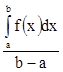 принято называть средним значением функции f(х) на [a, b].

               Область применения определенного интеграла очень широка. Его геометрические и физические интерпретации весьма разнообразны. С помощью определенного интеграла рассчитываются площади и объемы, центры тяжести объектов, путь, пройденный с переменной скоростью, массы неоднородных фигур и т.д., и т.п. Здесь мы

38

остановимся лишь на геометрической интерпретации определенного интеграла.

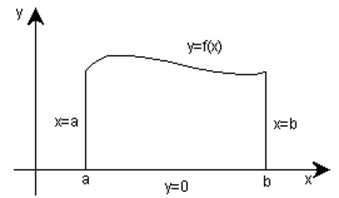
               Если на интервале [a, b] график функции у=f(х) лежит выше оси ОХ, то 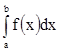 равен площади плоской фигуры, ограниченной линиями: х=а, х=b, у=0, у= f(х).

               В заключение подчеркнем еще раз очень важное обстоятельство, которое, может быть, было недостаточно выделено раньше: понятие определенного интеграла имеет смысл не для всякой функции. Интеграл 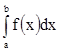 существует для функции, непрерывной на [a, b], или имеющей на [a, b] конечное число точек разрыва первого рода, но во всех остальных случаях необходима крайняя осторожность при вычислении 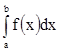. Есть возможность найти то, что на самом деле не существует.

Приведем пример:

Функция у= на[2, -1] не является непрерывной, в точке х=0 имеет разрыв второго рода: . Если формально подойти к вычислению 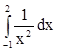, может возникнуть одна из следующих ситуаций:

1) формула Ньютона-Лейбница (6), которую здесь нельзя применять, дает 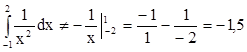. Число -1,5 никакого отношения к

39

интегралу 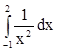, на самом деле равному бесконечности не имеет.

2) при замене интеграла какой-нибудь интегральной суммой вида (3) точка 0 может совпасть с x_i, а может и не совпасть; в первом случае программа откажется работать, а во втором случае – выдаст число, опять ничего общего с ответом не имеющее.

2. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ.

               Теорией вероятностей называется математическая наука, изучающая закономерности в случайных явлениях.

               Назовем эксперимент детерминированным, если при его повторении результаты совпадают, и стохастическим, если при его повторении результаты могут оказаться разными, т.е. точно предсказать результат эксперимента невозможно.

               Очевидно, в природе нет чисто детерминированных экспериментов, случайные отклонения неизбежно сопутствуют каждому закономерному явлению, но в ряде случаев этими отклонениями можно пренебречь.

2.1 Случайные события и вероятностные пространства.

               Пусть результатом какого-то стохастического эксперимента обязательно будет один и только один из исходов: w₁, w₂, w₃, ..., w_n, которые мы назовем элементарными. Каждому из элементарных исходов w_i поставим в соответствие число р _i

р_i³0 "i=1, 2, 3, ..., n;

р₁+ р₂+ ... + р_n=1.

Эта схема и называется вероятностным пространством эксперимента, числа р_i – вероятностями элементарных исходов w_i.

Если вероятностное пространство описывает какой-то реальный стохастический эксперимент, под вероятностью р_i подразумевают часть экспериментов, закончившихся исходом w_i при многократном повторении этого эксперимента.

Например, утверждение "вероятность того, что при подбрасывании двух игральных кубиков сумма выпавших очков составит шесть равна " означает: если два кубика будут подброшены n раз, то примерно m раз, где m= сумма выпавших очков составит шесть.

Рассмотрим множество всех элементарных исходов

W={w₁, w₂, w₃, ..., w_i, ..., w_n}.

40

пятидесяти лет назад, базируется на совершенно иной основе, а именно на формуле Ньютона-Лейбница:

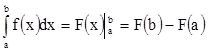,                                     (6)

где F(х) – одна из первообразных подынтегральной функции f(х), запись  - условная запись разности значений функции F(х) в двух точках a и b. Точку а принято называть нижним пределом интеграла, точку b – верхним пределом.