Методические указания к практическим занятиям по дисциплине "Высшая математика". Часть 2. Задачи для самостоятельного решения по теории вероятностей, страница 17

Проведем соответствующие арифметические действия и получим

Х	0	1	2	3	4	5
Р	0,168	0,360	0,309	0,132	0,028	0,003

m_x=np=5×0,3=1,5

=npq=5×0,3×0,7=1,05

=1,025

Пример 2:

Монета брошена десять раз. найти вероятность того, что герб выпадет не меньше восьми раз.

Решение:

n=10, р=0,5, q=0,5

50

2) ;

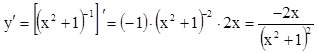 определена во всех точках числовой оси,

            =0 при х=0.

Функция может иметь экстремум только в точке х=0, в других точках у нее экстремума нет. Проверим, есть ли экстремум в (×) х=0.

При х<0 >0, при х>0 <0 Þ слева от точки х=0 функция возрастает, справа – убывает, в (×) х=0  у(х)= имеет max, y_max=у(0)=.

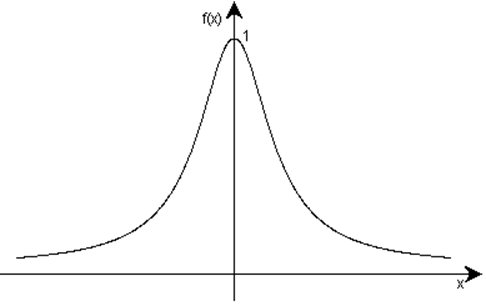
Строим график функции, учитывая:

            1) в (×) х=0 функция имеет max, y_max=1

            2) при х<0 у(х) возрастает (>0)

            3) при х>0 у(х) убывает (<0)

            4) у(х)= >0 "х (очевидно)

            5)

27

распределения, например, вычислять Р(Х=2)=, но при отсутствии вычислительной техники (лет 50 назад) процесс вычисления  все равно пришлось бы сводить к вычислению числа е в какой-то степени.

               Распределение Пуассона используется также, если случайная величина Х определяет количество каких-то событий за промежуток времени Dt, причем среднее число таких событий равно а и возрастает ровно в l раз, если в l раз увеличить промежуток времени.

Пример:

В конторе с 9 до 10 часов утра телефон в среднем звонит 4 раза. Найти вероятность того, что

1) в этот промежуток времени телефонных звонков не будет (Х=0)

2) телефонных звонков будет меньше трех (Х<3)

30 количество телефонных звонков будет больше шести (Х>6).

Решение:

1) Р(Х=0)=0,018

2) Р(Х<3)=Р(Х=0)+Р(Х=1)+Р(Х=2)=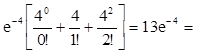0,234

3) Р(Х>6)=1-Р(Х£6)=1=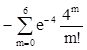

=1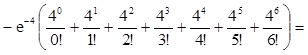0,111.

2.3.3 Нормальное распредление Гаусса.

Говорят, что непрерывная случайная величина Х распределена нормально с параметрами (m, s), если ее плотность распределения и функция распределния имеют вид:

 , ,

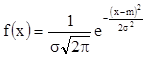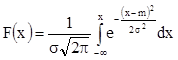где М(Х)=m, D(Х)= s².

При любых значениях m и s плотность и функция распределения случайной величины выражается через стандартные функции j(х) и F(х), значения которых затабулированы и приводятся во всех учебниках и справочниках по теории вероятностей:

52

Определение 4.

Точка х₀, отделяющая промежуток возрастания функции y=f(х) от промежутка убывания, называется точкой локального максимума этой функции.

Точка х₀, отделяющая промежуток убывания функции y=f(х) от промежутка возрастания, называется точкой локального минимума этой функции.

Точки максимума или минимума функции называются точками экстремума, значения функции в этих точках – экстремумами или экстремальными значениями. Иногда используется следующая терминология: функция y=f(х) имеет экстремум (max или min) в точке х₀.

На рисунке изображен график функции у=х³-х²-х+4.

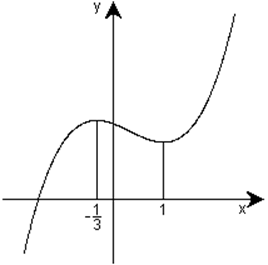
Эта функция возрастает на промежутках 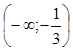 и , убывает на 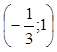. Каждый из этих промежутков является промежутком монотонности. В точках х= и х=1 функция имеет экстремумы: в точке х= - max, в точке х=1 – min.

               Известны следующие теоремы:

Теорема 1.

Если на промежутке <a,b> функция y=f(х) имеет производную и монотонна, то на этом промежутке производная функции не меняет знак:

y=f(х) имеет производную и убывает на <a,b> Û  £ 0 " х Î <a,b>,

25

арифметическим:  или . Какими бы не были законы распределения величин Х₁, Х₂, …, Х_n, закон распределения Х будет близок к нормальному (тем ближе, чем больше значение n). Это утверждение строго формулируется в законе больших чисел.

2.3.4 Закон больших чисел.

Центральная предельная теория.

Содержание закона больших чисел состоит в следующем: при очень большом числе случайных явлений их результат практически перестает быть случайным и может быть предсказан с большой степенью определенности. Приведем здесь одну из самых простых математических формулировок закона больших чисел, которая называется центральной предельной теорией для одинаково распределенных слагаемых: