Также, как и х0, А является числом, конечным или бесконечным.
Определение предела, совершенно строгое и ясное, очень часто при первом (а часто и при последующем) знакомстве вызывает впечатление чего-то туманного и непостижимого. Попробуем изложить в простой форме некоторые выводы из этого определения, которые часто помогают воспринять само определение.
Если х0 и А –
конечные числа, то равенство 
означает, что график
функции y=f(х) проходит через
точку с координатами (х0 ;А) и почти всегда f(х0)=А.
Если х0=+¥, А – конечное число, то равенство означает, что при достаточно больших
значениях х (при неограниченном возрастании х) значения f (х) сколь угодно мало
будут отличаться от А.
Если х0=+¥, А =+¥,
то равенство 
означает, что при неограниченном
возрастании аргумента х значения функции будут также неограниченно возрастать.
Если ...
Не будем перечислять все возможные варианты,
но проиллюстрируем графически понятие .
На рисунке 1 изображен график функции f(х)=
.
10
Вариант 2.
1. В киоске есть маркеры восьми различных цветов. Каким количеством способов можно выбрать пять маркеров различных цветов? Не обязательно различных?
2. Из колоды карт вынимают четыре карты.
Событие А – все карты одной масти.
Событие В – все карты черные.
Событие С – среди этих карт ровно один туз.
Дать описание событий А&В, А+В, 
&В, 
,
С&А, С+В.
3. В футбольном первенстве принимают участие 17 команд. Две команды, занявшие последние места, покидают лигу. При отсутствии какой-либо информации о подготовке команд, найти вероятности угадать
- кто покинет лигу
- кто войдет в тройку призеров, и кто покинет лигу
- кто займет первое, второе и третье места.
4. Три стрелка стреляют по мишени. Вероятность попадания первого стрелка равна 0.7, второго - 0.95, третьего - 0.75. Найти вероятности следующих событий:
- промахнулся хотя бы один стрелок.
- попал ровно один стрелок.
- попали ровно два стрелка.
- все трое промахнулись.
5. В пирамиде установлено 10 винтовок, четыре их которых имеют оптический прицел. Вероятность поражения мишени из винтовки с оптическим прицелом равна 0,95, а из винтовки без оптического прицела 0,8. Стрелок поразил мишень. Что вероятнее: была взята винтовка с оптическим прицелом или без него?
6. Вероятность успеха в одном эксперименте равна 0,6. Эксперимент проводится 10 раз. Найти вероятность того, что
- все десять результатов успешны
- хотя бы один результат неудачен
- ровно одна результат неудачен.
7. В ящике 5 белых и 8 черных шариков, одинаковых на ощупь. Наудачу вынимают пять шаров. Случайная величина Х – количество белых шаров среди вынутых. Построить ряд распределения для случайной величины Х, найти математическое ожидание, дисперсию и функцию распределения случайной величины.
8. Плотность распределения случайной величины
Х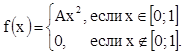 
.
Найти А, М(Х), D(Х), F(х), P(X<0,5). Р(Х>2).
9. Найти вероятность того, что при 500 бросаниях монеты герб выпадает не более 240 раз.
10. Случайная величина подчиняется нормальному закону распределения с математическим ожиданием m=5 и дисперсией 0,4. Найти вероятность того, что случайная величина
- будет меньше своего математического ожидания
- отклонится от математического ожидания более чем на единицу.
11. По схеме Бернулли было проведено 10 опытов, и из них в четырех произошло событие А. Найдите с надежностью g=0,8 доверительный интервал для вероятности события А.
12. Контрольные обмеры двадцати валиков дали следующие результаты: 7,39; 7,43; 7,54; 7,64; 7,40; 7,55; 7,40; 7,26; 7,42; 7,50; 7,32; 7,31; 7,28; 7,52; 7,46; 7,63; 7,38; 7,44; 7,52; 7,53. Дать точечные оценки для размера валика и его дисперсии.
67
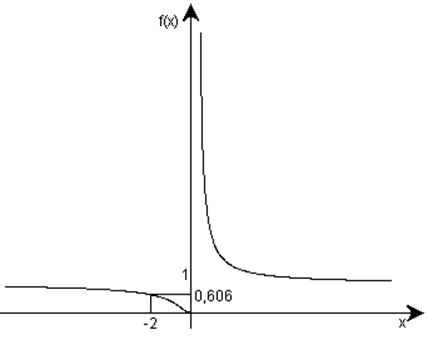
Рис. 3
Следует отметить, что 
не
существует, но если, рассматривая , рассмотреть два
варианта, для положительных и отрицательных х, 
и 
, то окажется, что 
,
.
Пределы, в которых при х®х0 рассматривают один из вариантов, x>х0 или х<х0, называется односторонними.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.