Методические указания к практическим занятиям по дисциплине "Высшая математика". Часть 2. Задачи для самостоятельного решения по теории вероятностей, страница 15

где в верхней строке перечислены в порядке возрастания все возможные значения Х, а в нижней – вероятности этих значений p_i=P(X=x_i). Очевидно, что .

Пример 1.

Брошены два игральных кубика. Сумма выпавших на двух кубиках очков – случайная величина Х, которая может принимать значения от 2 до 12. Построить ряд распределения Х.

Решение:

Здесь 36 элементарных исходов:

Обозначим их w_ij, где i – количество очков на первом кубике, j – на втором. Вероятность каждого из элементарных исходов р_ij=. Каждому значению случайной величины кроме Х=2 и Х=12 соответствует несколько элементарных исходов:

Х=2 « {w₁₁}

Х=3 « {w₁₂, w₂₁}

Х=4 « {w₁₃, w₂₂, w₃₁}

...

Х=10 « {w₄₆, w₅₅, w₆₄}

Х=11 « {w₅₆, w₆₅}

Х=12 « {w₆₆}

44

= F(х)+С,                                            (2)

где , С – любое постоянное число.

               "Взять неопределенный интеграл", то есть отыскать аналитическое выражение F(х) по заданной функции f(х) – задача, для решения которой часто требуются фантазия и определенные навыки. Мы не будем останавливаться на этом вопросе. Неопределенный интеграл используется лишь как инструмент для нахождения определенного интеграла, а при современном компьютерном обеспечении гораздо легче определенный интеграл вычислять непосредственно, используя любую из многочисленных стандартных программ. В тех случаях, когда значения неопределенного интеграла все-таки понадобятся, будем использовать таблицу неопределенных интегралов.

1.8.2. Определенный интеграл.

               Прежде чем ввести понятие "определенный интеграл", введем понятие "интегральная сумма функции f(х) на промежутке [a,b]". Интегральной суммой функции f(х) на [a,b] назовем число , полученное в результате следующих операций:

- выбираем целое число n>2;

- разбиваем произвольным образом [a,b] на n частей и находим длину каждой части Dх₁, Dх₂, …, Dх_i, …, Dх_n (очевидно,  - длине интервала).

 - в каждой части выбираем точку и обозначаем эти точки x₁, x₂, …, x_i, …, x_n.

- находим значения функции f(х) в этих точках: f(x₁), f(x₂), …, f(x_i), …, f(x_n).

- составляем выражение = f(x₁)×Dх₁+ f(x₂)×Dх₂+…+ f(x_i)×Dх_i+…+ f(x_n)×Dх_n и вычисляем его. Эта сумма

,                                               (3)

где Dх_i и x_i выбираются так, как указаны выше, и называется интегральной суммой функции f(х) на [a,b].

               Очевидно, различных интегральных сумм функции f(х) на [a,b] для одного и того же n будет бесконечно много. Тем не менее доказано,

33

нулевую вероятность. Заметим, однако, что для любого сколь угодно малого Dа вероятность непрерывной случайной величины Х попасть в промежуток (а-Dа; а+Dа) уже не обязана равняться нулю.

Рассмотрим, например, такую непрерывную случайную величину, как рост наугад взятого человека. Действительно, рассматривать вероятность того, что его рост окажется равным 177,0000 см, без малейшего отклонения, даже на тысячную долю миллиметра, неразумно хотя бы потому, что невозможно на практике измерить рост с такой точностью, тем более, что рост каждого человека колеблется в течение суток на 1¸2  мм. Поэтому для непрерывной случайной величины никогда не пытаются искать вероятность того, что она принимает какое-то конкретное значение, а рассматривают для нее только вероятность попадания в какой-то промежуток (a; b).

Рассмотрим непрерывную случайную величину, плотность распределения которой имеет следующий вид:

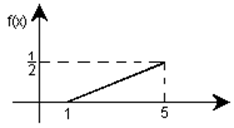
Здесь f(х)=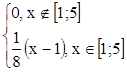

Очевидно Р(Х<1)=Р(Х>5)=0, то есть все значения рассматриваемой случайной величины заключены в промежутке [1; 5]. Найдем вероятность попадания случайной величины в несколько промежутков шириной 0,2: а) [1; 1,2], б) [2,5; 2,7], в) [4,8; 5].