Пусть y=f(х) – функция вещественной переменной; хÎХ; yÎY. Проведем на плоскости две взаимно перпендикулярные прямые и назовем их осями координат, или осью абсцисс и осью ординат. Ось абсцисс расположена горизонтально, ось ординат – вертикально. Точкой, соответствующей числу 0, выберем точку пересечния осей. На оси абсцисс отложим какое-то хÎХ на оси ординат отложим y=f(х) ÎY и восстановим перпендикуляры к осям из отмеченных точек до их пересечения. Множество точек пересечения таких перпендикуляров, полученных при всех хÎХ, называются графиком функции.
Наиболее распространенными способами задания функции f(х) являются:
- аналитический, при котором указывается формула, позволяющая по заданным значениям аргумента хÎХ получить соответствующее значение y=f(х) ÎY;
8
Вариант 4.
1. Каким количеством способов из 25 человек, входящих в научное общество, можно выбрать президента, вице-президента, ученого секретаря и казначея, если один человек может занимать только один пост?
2. В урне черные, белые и синие шары. Вынимают четыре шара.
Событие А – все шары белые.
Событие В – среди шаров ровно один белый.
Событие С – среди этих шаров хотя бы один синий.
Дать описание событий А&В, А+В, 
&В, 
,
С&А, С+В.
3. Участники игры зачеркивают на игровой карте 5 чисел из 20. Во время розыгрыша объявляют пять выигравших номеров. Найти вероятность для игрока
- не угадать ни одного числа
- угадать хотя бы три числа
- угадать ровно четыре числа.
4. Три станка работают независимо друг от друга. Вероятность того, что первый станок проработает смену без наладки 0,8, второй – 0,9, а третий – 0,95. Найти вероятности следующих событий:
- все станки проработают смену без наладки
- все станки потребуют наладку
- хотя бы один станок проработает смену без наладки
- ровно два станка проработают смену без наладки.
5. В спартакиаде участвуют: из первой группы 4 студента, из второй – 6, из третьей – 5. Студент первой группы попадает в сборную института с вероятностью 0,9, из второй – с вероятностью 0,7, из третьей – с вероятностью 0,8. Студент попал в сборную. Найти вероятность того, что студент учится в третьей группе.
6. Вероятность успеха в одном эксперименте равна 0,75. Эксперимент проводится 6 раз. Найти вероятность того, что
- все шесть результатов успешны
- хотя бы одна неудача
- ровно один успех.
7. В ящике 2 белых и 3 синих шарика, одинаковых на ощупь. Наудачу вынимают три шара. Случайная величина Х – количество белых шаров среди вынутых. Построить ряд распределения для случайной величины Х, найти математическое ожидание, дисперсию и функцию распределения случайной величины.
8. Плотность распределения случайной величины
Х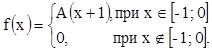 
.
Найти А, М(Х), D(Х), F(х), P(X< -0,5). Р(Х>2).
9. Найти вероятность того, что при 200 бросаниях монеты герб выпадает не более 90 раз.
10. Случайная величина подчиняется нормальному закону распределения с математическим ожиданием m=15 и дисперсией 20. Найти вероятность того, что случайная величина
- отрицательна
- больше 35.
11. По схеме Бернулли было проведено 9 опытов, и из них в четырех произошло событие А. Найдите с надежностью g=0,85 доверительный интервал для вероятности события А.
12. Контрольные обмеры двадцати валиков дали следующие результаты: 7,39; 7,43; 7,54; 7,64; 7,40; 7,55; 7,40; 7,26; 7,42; 7,50; 7,32; 7,31; 7,28; 7,52; 7,46; 7,63; 7,38; 7,44; 7,52; 7,53. Дать точечные оценки для размера валика и его дисперсии.
69
основного в анализе понятия предел функции
начнем с обозначения и определения. Предел функции обозначается 
и читается: предел функции y=f(х) при х стремящемся
к х0 (х0 – число, конечное или ¥).
Для функции y=f(х), определенной на
множестве Х, равенство 
означает, что
" 
$ 
: х Î Ç Х Þ
f(х) Î 
. (*)
(для любой e-окрестности точки А найдется d-окрестность точки х0, такая, что для всех х, попадающих в эту d-окрестность и принадлежащих области определения Х, соответствующее значение f(х) попадет в e-окрестность точки А).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.