6. Составить любую интегральную сумму при n=4 для интеграла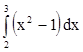 
. Сравнить ее значение с точным значением
интеграла.
7. Найти 
в
произвольной точке и точке М0 (1,4,-2), если 
.
8. Найти экстремумы функции 
.
9. Цены на товар три раза повышались на 4%. На сколько процентов возросла цена по сравнению с первоначальной? На сколько процентов надо уменьшить достигнутую цену, чтобы она стала равна первоначальной?
10. Банк выплачивает клиентам 12% годового дохода. Какой процент годового дохода можно получить, ежемесячно снимая проценты и добавляя их к вкладу? До какой максимальной величины можно довести процент годового дохода? Все операции проводятся бесплатно.
62
Теорема 5.
]
=А, 
=В.
Тогда 
.
Замечания: 1) если А>1, В=+¥, то 
;
2) если 0<A<1, В=+¥, то 
;
3) если А>1, В= -¥, то 
;
4) если 0<A<1, В= -¥, то 
;
5) теорема 5 не работает, если 5.1 А=1, В=¥,
или 5.2 А=0, В=0,
или 5.3 А=¥, В=¥.
Все варианты, при которых не работают
теоремы, в символическом виде записываются [+¥ - ¥], [0×¥], 
, 
, [1¥], [00], [¥0] и называются
неопределенностями.
Перечислив основные теоремы о пределах, дадим некоторые сведения о пределах элементарных функций.
Доказано, что для функций f(x)=xn, f(x)=ах,
f(x)=logах, f(x)=sinх, f(x)=cosх, f(x)=tgх, f(x)=ctgх, f(x)=arcsinх,
f(x)=arccosх, f(x)=arctgх, f(x)=arcctgх 
, если
х0ÎХ – области
определения функции.
Если х0ÏХ, но является точкой сгущения множества Х, для всех перечисленных функций значения пределов также известны.
Например: 
(при а>1),
,
не
существует.
Вычисление предела 
произвольной функции начинают с
подстановки х0 в функцию, стоящую под знаком предела. Если в
результате подстановки получено конечное число, оно и является ответом. (данная
рекомендация является достаточно грубой и в некоторых случаях даже может
оказаться некорректной, но тем не менее очень широко используется, особенно в
простейших случаях)
Если в результате подстановки получается один из вариантов, предусмотренный в первых пунктах замечаний к теоремам о пределах,
15
Вариант 9.
1. Построить один из возможных вариантов
графика функции у=f(х),
для которой 
, 
, 
, 
.
2. Вычислить
, 
, 
,
, 
, 
.
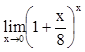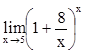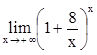3. Найти точки разрыва, асимптоты, интервалы
монотонности и экстремумы функций 
, 
. Построить графики функций.
4. Вычислить приближенно 
, используя пять слагаемых в формуле
Тейлора. Сравнить с точным значением.
5. Вычислить по формуле Ньютона-Лейбница ,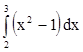 
.
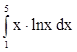6. Составить любую интегральную сумму при n=4 для интеграла 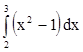. Сравнить ее значение с точным значением
интеграла.
7. Найти в
произвольной точке и точке М0 (1,4,-2), если .
8. Найти экстремумы функции 
.
9. Цены на товар три раза повышались на 4%. На сколько процентов возросла цена по сравнению с первоначальной? На сколько процентов надо уменьшить достигнутую цену, чтобы она стала равна первоначальной?
10. Банк выплачивает клиентам 12% годового дохода. Какой процент годового дохода можно получить, ежемесячно снимая проценты и добавляя их к вкладу? До какой максимальной величины можно довести процент годового дохода? Все операции проводятся бесплатно.
64
" 
$ 
: х Î Ç Х Þ
f(х) Î . (***)
Рассмотрим функцию y=f(х), график которой изображен на рисунке 4.
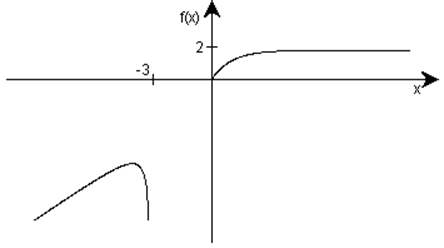
Рис. 4
Из вида графика следует, что 
, 
, 
и 
не
могут рассматриваться, т.к. при х, близких к нулю, но меньших нуля, а также при
х, близких к –3, но больших, чем –3, функция y=f(х) не определена.
Стоит отметить, что для этой функции 
; 
.
Для функции, график которой изображен на рисунке 5
, 
.
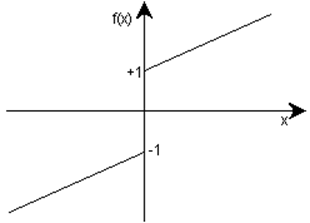
Рис. 5
На практике при вычислении предела конкретной функции,
13
Вариант 1
1. В магазине 10 сортов пирожных. Каким количеством способов можно выбрать 6 разных? Каким количеством способов можно выбрать 6 пирожных, не обязательно разных?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.