Рис. 2.1

Рис. 2.2
Математическая модель манипулятора учитывает кинематические связи, динамические взаимодействия инерционных, центробежных, кориолисовых и гравитационных моментов, внешние моменты исполнительных механизмов. В звеньях манипулятора используются сервопривода переменного тока. При построении математической модели приняты следующие допущения: отсутствуют люфты между валами двигателей и звеньями манипулятора; отсутствуют упругие деформации в приводах, передаточных механизмах и звеньях манипулятора; ошибки квантования на выходе цифровых систем управления электроприводами незначительны.
Динамика механической части манипулятора описывается нелинейным векторно-матричным уравнением 2-го порядка:
![]() ,
(2.1)
,
(2.1)
где ![]() - матрица коэффициентов
инерции, зависящая от вектора
- матрица коэффициентов
инерции, зависящая от вектора ![]() ;
; ![]() - вектор обобщенных
координат;
- вектор обобщенных
координат; ![]() - вектор обобщенных
скоростей;
- вектор обобщенных
скоростей; ![]() - вектор моментов сил
инерции, зависящий от векторов
- вектор моментов сил
инерции, зависящий от векторов![]() ,
, ![]() ;
; ![]() -
вектор моментов сил тяжести, зависящий от вектора
-
вектор моментов сил тяжести, зависящий от вектора ![]() ;
; ![]() -
вектор моментов трения,
-
вектор моментов трения, ![]() -
вектор обобщенных моментов.
-
вектор обобщенных моментов.
В развернутом виде система уравнений (2.1) приведена в [5] и в [7]. Подробный вывод уравнений дан в [7].
Динамические характеристики манипулятора зависят от его текущей пространственной конфигурации и изменяются в процессе манипулирования. Исходное расположение звеньев задается соответствующими начальными условиями для системы (2.1).
При
исследовании замкнутой системы управления манипулятором по координатам ![]() уравнение (2.1) необходимо дополнить
уравнениями
уравнение (2.1) необходимо дополнить
уравнениями
 |
электроприводов,
регуляторов координат, по которым реализуются обратные связи. Ориентируясь на
трехконтурные системы каждой из координат ![]() ,
выполненных по принципу подчиненного управления, необходимо для каждого из
каналов управления дополнить уравнение (2.1) уравнениями регуляторов положения,
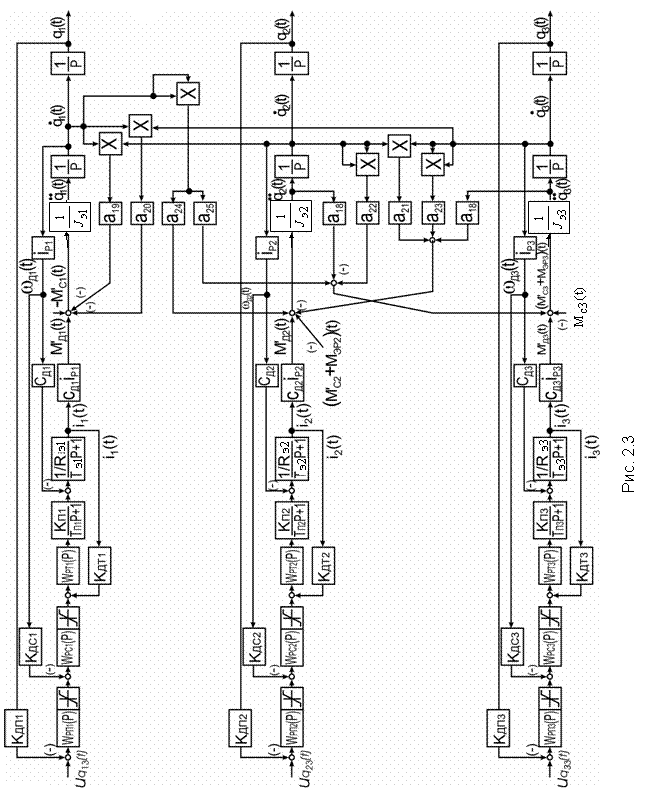
скорости и тока электродвигателя соответственно. Структурная схема системы
управления трехзвенным манипулятором показана на рис. 2.3.
,
выполненных по принципу подчиненного управления, необходимо для каждого из
каналов управления дополнить уравнение (2.1) уравнениями регуляторов положения,
скорости и тока электродвигателя соответственно. Структурная схема системы
управления трехзвенным манипулятором показана на рис. 2.3.
Расчет
параметров системы может быть выполнен в соответствии с пособием [5] .
Регуляторы положения и скорости принимаются П- или
ПИ-регуляторами.
2.2. Порядок выполнения работы
1.Ознакомиться с техническим описанием комплектных электроприводов и датчиков.
2. Составить математическую модель манипулятора с учетом электроприводов и передаточных механизмов.
3. Рассчитать систему управления в соответствии с вариантом задания.
4. Выполнить исследование динамических характеристик системы управления при заданных управляющих и возмущающих воздействиях, видах регуляторов, номерах звеньев манипулятора.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.