Основы проектирования и расчета судового валопровода, страница 34

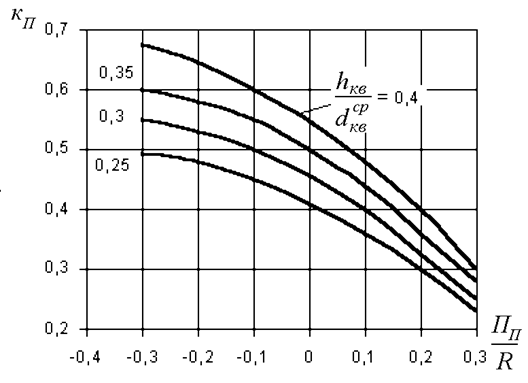
Рис. 5.35. Зависимость

Каких-либо обоснований применения указанных способов приведения коленчатого вала к дискретному виду нет. По этой причине последний способ можно считать более точным и перспективным только по тем соображениям, что расчетная модель коленчатого вала позволяет учитывать конструктивные особенности колена. При таком способе аппроксимации в центре шатунной шейки располагается приведенная к радиусу кривошипа масса неуравновешенных частей колена , а в серединах коренных шеек – 0,5, где ,  и  – соответственно, неуравновешенно- и уравновешенно вращающиеся массы колена вала и шатуна;  – коэффициент, входящий в формулу (5.28). Между собой массы связаны соединениями, их податливость вдвое меньше осевой податливости всего колена.

Расчет осевых колебаний в безразмерных параметрах выполняют традиционно по методу Терских.

5.11.3. Особенности расчета осевых колебаний

Как уже отмечалось, уравнения свободных крутильных и осевых колебаний в общем случае имеют одинаковый вид. Поэтому расчет этих колебаний может выполняться по одним и тем же программам.

По сравнению с предыдущим расчет резонансных колебаний имеет свои особенности. Прежде всего они касаются определения сил, выражающих осевые колебания. Обычно принято рассматривать силы, которые обусловлены работой ДВС и гребного винта.

Силовой анализ кривошипно-шатунного механизма дает радиальную силу , которая приложена к шатунной шейке. Под действием этой силы колено вала изгибается. Деформация изгиба сопровождается продольным укорочением или удлинением колена. Эквивалентная последней деформации осевая сила  выражается через передаточную функцию  простой зависимостью

.

Для вычисления передаточной функции чаще всего пользуются формулой

,

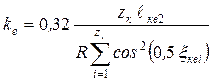где  – число кривошипов коленчатого вала;  – угол между соседними кривошипами, замеренный по направлению вращения вала.

Обращает на себя внимание тот факт, что величина деформации коленчатого вала в осевом направлении зависит от заклинки его кривошипов. Такое свойство коленчатых валов подтверждено экспериментально.

Радиальная сила является периодической функцией угла поворота кривошипа. Известно, что такую функцию можно подвергнуть гармоническому анализу и представить в виде тригонометрического ряда. Параметры ряда вычисляют по формулам Бесселя точно так же, как для крутящего момента. При этом для V-образных двигателей, где на шатунную шейку работают два цилиндра, разложению в ряд Фурье подвергают суммарную радиальную силу. После гармонического анализа радиальную силу (то же самое, что и эквивалентную осевую силу) представляют в виде совокупности отдельных гармоник. Порядки гармонических составляющих кратны числу вспышек за один оборот коленчатого вала и для четырех- и двухтактных двигателей полностью отвечают значениям, приведенным в параграфе 5.10.4.

Пульсирующий характер упора гребного винта установлен натурными замерами. Величина пульсаций зависит от множества факторов. Среди них отмечают форму кормовой оконечности судна, размещение гребного винта в кормовом подзоре, угол наклона линии валопровода, форму лопасти, осадку судна. В теоретическом плане учесть все перечисленные геометрические и эксплуатационные факторы не представляется возможным. Поэтому для приближенной оценки отдельных гармоник переменного упора гребного винта чаще всего прибегают к справочным данным. В табл. 5.9 приведены значения гармонических составляющих в зависимости от среднего упора .

Таблица 5.9

Гармонические составляющие упора гребного винта