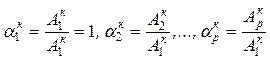Основы проектирования и расчета судового валопровода, страница 23

.

В вычислительном отношении изложенный алгоритм является нетривиальной операцией, реализуемой только на ЭВМ. Существуют компактные программы, которые позволяют автоматически формировать исходные матрицы, управлять шагом итерации, вычислять частоты свободных колебаний и соответствующие им безразмерные амплитуды [25].

Наряду с рассмотренным алгоритмом в инженерной практике до сих пор применяются методы расчета свободных колебаний, ориентированные на ручной счет. Последнее обстоятельство вынуждает приводить параметры дискретной модели к безразмерному виду с помощью следующих зависимостей

;  ,

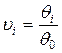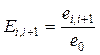где  и  – постоянные расчетной модели, обычно момент инерции КШМ ( = ) и податливость колена вала (=).

Опуская промежуточные выводы, приведем конечные зависимости метода цепных дробей (метод Терских) и метода остатка  (метод Толле). Фундаментальным понятием уравнений этих методов является стойкость массы, численно равная произведению массы на квадрат частоты ее колебаний со знаком минус:

,

где  – квадрат безразмерной частоты. Связь  с технической частотой устанавливается соотношением

,

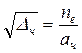где

.

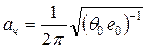Частотное уравнение в форме цепной дроби представляет собой сумму параметров системы в той последовательности, в какой они встречаются в расчетной модели, начиная с последнего элемента. Для  – массовой простой модели уравнение свободных колебаний имеет вид

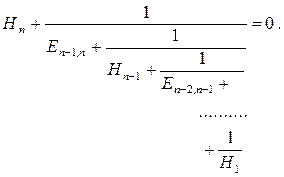                                           (5.40)

Уравнение свободных колебаний разветвленной модели, показанной на рис. 5.29, может быть написано аналогично (5.40), однако в этом случае вместо стойкости -й массы в уравнение вводится стойкость ответвления

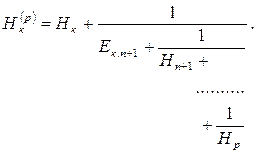
После этого заданную разветвленную систему можно рассматривать как простую, для которой уравнение (5.40) принимает вид

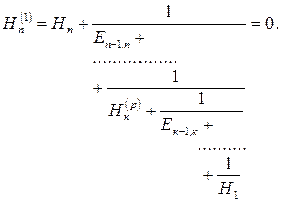                                           (5.41)

Левая часть уравнений (5.40) и (5.41) обращается в нуль тогда, когда входящий в нее квадрат безразмерной частоты  соответствует любому из корней уравнения, число которых на единицу меньше числа масс. Следовательно, путем подстановок пробных значений  в исходные уравнения удается отыскать все интересующие частоты свободных колебаний. Расчеты выполняются в табличной форме.

После определения искомой частоты вычисляются безразмерные амплитуды упругого момента  и амплитуды колебаний . Выполнение этой процедуры осуществляется сначала для основной группы элементов расчетной модели по зависимостям

                           ;  ,                   (5.42)

где  – стойкость части системы от -й до 1-й массы;  – податливость части системы от соединения ,+1 до 1-й массы.

Затем определяются амплитуды моментов и колебаний в пределах ответвления, начиная от места ответвления и кончая его свободным концом, по формулам

;  .

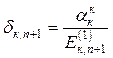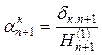Аналогичным способом может быть записано частное уравнение для расчетной модели с двумя ответвлениями.

Решение задачи о свободных колебаниях дискретных моделей по методу остатка основано на равенстве нулю упругого момента последнего несуществующего соединения ,. Этот момент называется остаточным моментом , его величина .

Остаточный момент подсчитывают по рекуррентным формулам, последовательно рассматривая все параметры модели, начиная с первого:

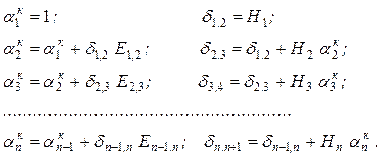
Проведя несколько пробных определений остаточного момента, находят то значение , при котором  = 0. Это значение  будет равно искомой частоте свободных колебаний. Расчет остаточного момента производится в таблице, носящей имя авторы метода. Погрешность вычислений частоты задается обычно в пределах (1¸2)%.

Расчетные зависимости методов Терских и Толле имеют простой и наглядный алгоритм вычислений. Поэтому они могут быть реализованы без ЭВМ, хотя программирование этих зависимостей не затруднений.

Таким образом, расчет свободных крутильных колебаний судового валопровода сводится к определению собственных частот и присущих им амплитуд колебаний масс  и амплитуд упругих моментов  в безразмерной форме. Их значения за редуктором (мультипликатором) находят из соотношений