Крутящий момент так же, как тангенциальная сила, является периодической функцией угла поворота коленчатого вала. Зависимость момента от суммарного действия сил давления газов, сил инерции и тяжести движущихся масс устанавливается численно в виде совокупности последовательных ординат и нередко задается графически. Такую периодическую кривую удобно представить в форме тригонометрического ряда посредством гармонического анализа. Другими словами, крутящий момент кривошипа можно выразить так
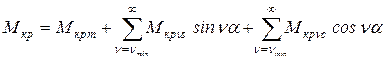 , (5.43)
, (5.43)
где ![]() – среднее значение момента;
– среднее значение момента; ![]() и
и ![]() –
амплитуды синусных и косинусных составляющих;
–
амплитуды синусных и косинусных составляющих; ![]() – угол поворота
коленчатого вала;
– угол поворота
коленчатого вала; ![]() – минимальный порядок: для
четырехтактных ДВС
– минимальный порядок: для
четырехтактных ДВС ![]() =0,5, для двухтактных двигателей
=0,5, для двухтактных двигателей ![]() = 1.
= 1.
Параметры формулы (5.43) вычисляют по уравнениям Бесселя.
Предварительно отрезок кривой крутящего момента, соответствующий периоду
рабочего процесса ДВС, делят на ![]() равных частей, обычно
равных частей, обычно ![]() >
6
>
6![]() , где
, где ![]() –
максимальный порядок гармонических составляющих (рис. 5.31). Если ординаты
точек деления
–
максимальный порядок гармонических составляющих (рис. 5.31). Если ординаты
точек деления ![]() ¹
(
¹
(![]() = 1, 2,…,
= 1, 2,…, ![]() +1) при
условии
+1) при
условии ![]() , то
, то
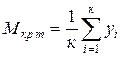 ;
; 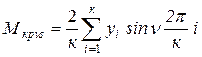 ;
;
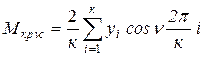 .
.
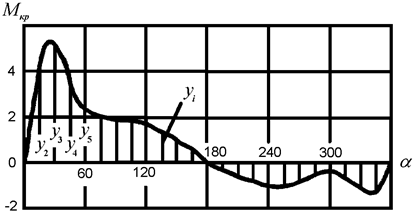
Рис. 5.31. Дискретизация крутящего момента двухтактного двигателя
Расчет по формулам Бесселя производят последовательно для
всех интересующих порядков. С точки зрения динамической нагруженности
валопровода достаточно ограничиться рассмотрением только низших гармоник до ![]() = 12¸15.
Объясняется это тем, что тригонометрический ряд (5.43) затухнет, хотя и
медленно. По этой причине для высоких порядков амплитуды гармонических моментов
становятся незначительными.
= 12¸15.
Объясняется это тем, что тригонометрический ряд (5.43) затухнет, хотя и
медленно. По этой причине для высоких порядков амплитуды гармонических моментов
становятся незначительными.
После вычисления всех коэффициентов ![]() и
и ![]() тригонометрический
ряд Фурье записывают в более простом виде:
тригонометрический
ряд Фурье записывают в более простом виде:
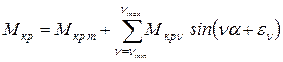 , (5.44)
, (5.44)
где
![]() ,
, 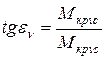 .
.
Изложенный порядок определения вынужденных моментов легко реализуется на ЭВМ. В этом случае исходными данными служат ординаты тангенциальной силы в функции угла поворота коленчатого вала для всех резонансных режимов эксплуатации валопровода.
На ранних стадиях проектирования значения амплитуд гармонических
моментов (5.44) можно оценить приближенно по графическим зависимостям на рис. 5.32
[36]. Пользуясь этими графиками, определяют гармонический коэффициент ![]() в функции среднего индикаторного давления
в функции среднего индикаторного давления ![]() . Его величину предварительно подсчитывают
по формуле
. Его величину предварительно подсчитывают
по формуле
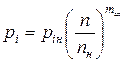 ,
,
где ![]() – среднее индикаторное давление,
соответствующее номинальной частоте вращения
– среднее индикаторное давление,
соответствующее номинальной частоте вращения ![]() ;
; ![]() – частота вращения коленчатого вала на
резонансном режиме;
– частота вращения коленчатого вала на
резонансном режиме; ![]() – показатель степени,
– показатель степени, ![]() = 2 при работе двигателя по винтовой
характеристике.
= 2 при работе двигателя по винтовой
характеристике.
С учетом гармонического коэффициента амплитуда вынуждающего момента будет:
для рядного ДВС
![]() ;
;
для V-образного двигателя
![]() ,
,
где ![]() – угол между вспышками в
цилиндрах одного кривошипно-шатунного механизма.
– угол между вспышками в
цилиндрах одного кривошипно-шатунного механизма.
Переменный крутящий момент, обусловленный работой гребного винта в неравномерном потоке воды, может быть также представлен в виде совокупности отдельных гармонических составляющих. При отсутствии более точных данных амплитуды гармонических моментов определяются ориентировочно по справочным данным. В табл. 5.7 приведены значения гармоник в зависимости от среднего крутящего момента.
Таким образом, определение моментов, которые вызывают крутильные колебания, по существу, сводится к получению гармонических составляющих, имеющих наибольшие амплитуды. На этом основании напряжения от колебаний вычисляются для каждой гармоники в отдельности, после чего результаты суммируют.
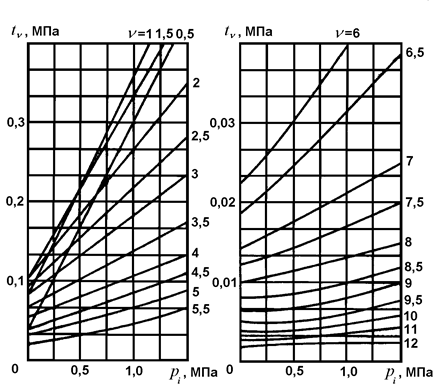
Рис. 5.32. Гармонические коэффициенты судового дизеля
Таблица 5.7
Гармоники крутящего момента от гребного винта
|
Число лопастей |
Порядок |
Амплитуда |
Порядок |
Амплитуда |
|
3 4 5 |
3 4 5 |
0,042 Mкр m 0,076 Mкр m 0,090 Mкр m |
6 8 10 |
0,043 Mкр m 0,026 Mкр m 0,015 Mкр m |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.