Основы проектирования и расчета судового валопровода, страница 31

5.11.2. Составление расчетной модели

Для расчета осевых колебаний судовой валопровод заменяется дискретной моделью. Последняя составляется аналогично модели для крутильных колебаний с тем отличием, что вместо величин моментов инерции вращающихся масс и крутильных податливостей рассматриваются величины масс  и осевые податливости .

Безразмерные параметры расчетной модели для исследования осевых колебаний обозначают следующими символами:

– безразмерная масса

;

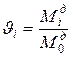– безразмерная осевая податливость

,

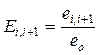где  – обычно масса колена вала;  – его податливость.

Расчетная модель, как и в случае крутильных колебаний, изображается совокупностью кружков, соединенных между собой отрезками прямых. Площади кружков приблизительно пропорциональны , а длины отрезков точно пропорциональны осевым податливостям участков валопровода .

На рис. 5.34 в качестве примера представлена дискретная модель судового валопровода для расчета осевых колебаний. Ответвление аппроксимирует главный упорный подшипник с параметрами  и , характеризующими упругомассовые свойства упругого подшипника, упругого гребня и части упругого вала. Жесткая заделка конца ответвления соответствует бесконечно большой массе корпуса судна. Наклон отрезка  выбран произвольно (возникающая в нем упругая сила направлена всегда вдоль оси вала).

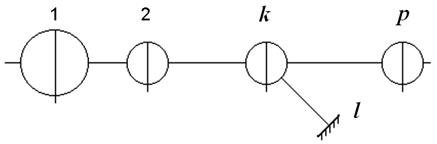
Рис. 5.34. Дискретная модель судового валопровода

Данная модель будет тождественна, если отсутствует перекладка зазора в упорном подшипнике. Если в результате предварительного расчета обнаружится, что амплитуда осевой упругой силы на участке, где расположен гребень упорного подшипника, превышает среднее значение упора гребного винта, то в нем возникает перекладка зазора. В этом случае массу корпуса упорного подшипника следует учитывать особо, рассматривая ее в качестве промежуточной массы ответвления. Последняя будет связана с предыдущей соединением с зазором, которое всегда обладает нелинейной характеристикой, а поэтому вся система становится нелинейной.

Примерно также идеализируется демпфер осевых колебаний. Он заменяется тремя массами: одна – масса гребня (), другая– масса корпуса демпфера (), третья – масса основания (жесткое защемление). Все массы связаны соответствующими жесткостями, кроме того, в схеме присутствует демпфирующий элемент .

При расчете осевых колебаний наличие редуктора в системе не приводит к трансформации упругомассовых свойств. Между тем, наличие в установке редуктора с прямозубыми колесами (если не считать сил трения) изолирует ведущую часть валопровода от ведомой. Значительно более сложной получается дискретная модель в случае косозубых передач, так как при наличии перекладки зазора в зубчатом зацеплении перекладки зазора в зубчатом зацеплении осевые колебания становятся нелинейными.

При составлении дискретной модели сосредоточенными условно считают такие массы деталей, длина которых менее полутора-двух диаметров вала. Деформацией таких масс можно пренебречь и учитывать только их инерционные свойства. Такие массы сосредоточивают в центрах тяжести рассматриваемых элементов. К сосредоточенным массам могут быть отнесены: гребной винт, колеса редуктора, маховики.

Масса гребного винта оценивается массой самого винта  и массой увлекаемой им воды :

.

Ориентировочно массу М_М можно определить по формуле (5.10) или так

,

где  – масса ступицы гребного винта, кг,

;

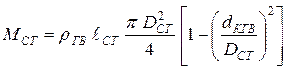 – масса лопастей гребного винта, кг,

,

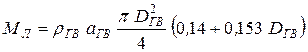 – длина ступицы, м;  – наружный диаметр ступицы, м;  – средний диаметр конуса гребного вала, м;  – дисковое отношение;  – диаметр гребного винта, м;  – плотность материала ступицы и лопасти.

Массу увлекаемой винтом воды принимают в пределах                           = (0,4÷0,6)  или рассчитывают по формуле

,

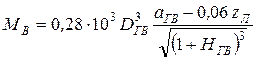где  – шаговое отношение;  – число лопастей.