Основы проектирования и расчета судового валопровода, страница 30

Установка демпфера приводит к изменению дискретной модели судового валопровода, поэтому сначала подбирается демпфер, а затем осуществляется пересчет свободных и резонансных колебаний. При этом момент инерции массы демпфера, присоединенного к коленчатому валу, рекомендуется задавать равным

,

где  – момент инерции корпуса демпфера.

В демпферах сухого трения энергия проскальзывания маховика относительно корпуса поглощается пакетами цилиндрических пружин. Пакеты устанавливают в отверстия, одна половина которых расположена в маховике, а другая – в корпусе. Пространство вокруг пружин заполняется маслом. Существуют конструкции демпферов, в качестве поглощающих элементов которых использованы фрикционные диски, прижимаемые к поверхностям трения пружинами. Несмотря на простоту конструкции, демпферы сухого трения не находят широкого распространения ввиду своей ненадежности.

5.11. Расчет осевых колебаний

5.11.1. Сущность осевых колебаний

При осевых колебаниях все точки валопровода совершают возвратно-поступательные перемещения вдоль своей оси. При этом в сечениях валопровода возникают деформации сжатия–растяжения, которые нередко являются причинами: повышенной вибрации, интенсивного износа упорного подшипника; фреттинг–коррозии конических сопрягаемых поверхностей, поломок коленчатых валов, обрывов нащечных противовесов, смещения обмоток якоря в генераторах. Осевые колебания реально существуют и заслуживают внимания особенно в судовых установках с длинноходными ДВС, у которых отношение  составляет 3÷4,4. Как известно, у таких двигателей отсутствуют перекрытие шеек коленчатого вала, вследствие чего его податливость в осевом направлении увеличивается, соответственно растет вероятность появления опасных резонансов в диапазоне эксплуатационных частот вращения.

Своим возникновением осевые колебания обязаны:

– радиальным силам, действующим на шатунные шейки коленчатого вала;

– осевой силе в редукторе с косозубыми колесами;

– переменной составляющей упора гребного винта.

Осевые колебания могут возникать также от вибрации корпуса судна, несоосности подшипников валопровода, их неравномерного износа и деформации фундаментов.

При расчете осевых колебаний судовой валопровод заменяется дискретной моделью, состоящей из ряда упругосвязанных сосредоточенных масс. Дифференциальные уравнения, описывающие свободные и вынужденные осевые колебания таких систем, не отличаются от уравнений, свойственных крутильным колебаниям, если вместо угловых перемещений масс рассматривать перемещения линейные, моменты инерции масс  заменить массами  (кг), а крутильные податливости – осевыми податливостями (м×Н^-1). Сохраняя те же обозначения и для остальных параметров, частное уравнение осевых колебаний можно записать как в матричной форме (5.39), так и в виде цепной дроби (5.40). Подобно этому форма свободных колебаний, т.е. совокупность амплитуд перемещений масс, определится по уравнениям (5.38) и (5.42).

Используя аналогию между крутильными и осевыми колебаниями, можно предположить, что валопровод в колебательном отношении не связан с корпусом судна. В действительности такая связь осуществляется упорным подшипником. Если упорный подшипник с присоединенной к нему массой валопровода представляет -ю массу дискретной модели, то корпус судна можно рассматривать как некоторую массу , присоединенную к упорному подшипнику упругим соединением с осевой податливостью . Эта податливость определяется деформацией корпуса упругого подшипника и фундамента, который связывает подшипник с корпусом судна. Таким образом, корпус судна можно рассматривать как ответвление от основной системы. При этом  ® ¥, так как масса корпуса судна существенно больше массы всего валопровода. В этом случае стойкость ответвления будет иметь вид:

.

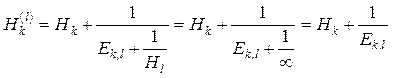Отметим еще одно отличие, касающееся форм свободных крутильных и осевых колебаний. Для осевых колебаний первой формы все амплитуды масс имеют одинаковый знак. Вторая форма колебаний имеет одну перемену знака амплитуд, третья – две и т.п.