Основы проектирования и расчета судового валопровода, страница 20

Частота свободных изгибных колебаний в горизонтальной плоскости определяется на основании рассчитанной величины  и зазора в дейдвудном подшипнике  по формуле

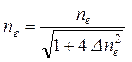                                          .                                 (5.27)

Несмотря на приближенный характер и очевидные допущения второй метод расчета изгибных колебаний стал общепризнанным.

5.10. Расчет крутильных колебаний

5.10.1. Общие понятия о крутильных колебаниях

Крутильными называют такие колебания системы, при которых все ее точки совершают движения переменного направления по дугам окружностей вокруг неподвижной оси. Возникающие при этом в валопроводе знакопеременные напряжения в некоторых случаях могут превысить предел усталости материала вала и вызвать его разрушения, а также быть причиной поломки муфт, зубчатых колес редуктора и других, связанных с ними, деталей. Вибрации двигателей и отдельных конструкций корпуса судна также могут быть следствием крутильных колебаний валопровода.

Источником крутильных колебаний служат переменные крутящие моменты, действующие в отдельных элементах валопровода: кривошипы коленчатого вала ДВС, гребной винт и пр.

5.10.2. Составление расчетной модели

Расчетная модель представляет собой совокупность чередующихся дискретных масс с моментами инерции  ( номер массы) и соединений, лишенных массовых свойств и наделенных только крутильной податливостью  (индексы указывают на номер масс, ограничивающих этот участок).

В принятом условном обозначении крутильной модели (рис. 5.25) массы изображаются кружками, площадь которых примерно пропорциональна их моментам инерции. Отрезки прямой между центрами кружков должны быть точно пропорциональны крутильным податливостям этих участков.

В зависимости от характера системы расчетные модели разделяются на простые, разветвленные и кольцевые (рис. 5.26). Кольцевые модели встречаются редко, поэтому далее они не рассматриваются.

Особую группу составляют системы с редукторами или мультипликаторами. Чтобы привести указанные системы к расчетной модели, моменты инерции масс за редуктором (мультипликатором) делятся, а крутильные податливости умножаются на квадрат передаточного отношения :

;    .

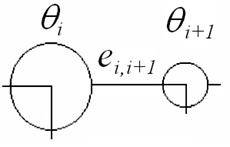
Рис. 5.25. Расчетная модель крутильных колебаний

Под передаточным отношением понимают отношение частоты вращения коленчатого вала к частоте вращения гребного винта. Для редуктора  > 1, для мультипликатора  < 1.

Параметры расчетной модели вычисляются следующим образом.

Момент инерции кривошипно-шатунного механизма (КШМ) относительно оси вращения коленчатого вала обычно сосредоточивают в центре шатунной шейки, а его численное значение определяют по формуле

                     ,                (5.28)

где  – момент инерции уравновешенно вращающейся части колена вала, кг×м²;  – радиус кривошипа, м;  – масса поршня, штока и крейцкопфа, кг;  – масса шатуна, кг;  – коэффициент, характеризующий отношение массы вращающейся части шатуна ко всей его массе.

Для крейцкопфных ДВС коэффициент  » 0,5; для тронковых двигателей его значение подсчитывается по формуле

,

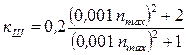где  – максимальная частота вращения вала, мин^-1.

В случае отсутствия всех необходимых данных ориентировочное определение  с погрешностью не более 10% можно произвести по формуле Терских:

,

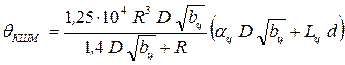где  – диаметр цилиндра, м;  – средний диаметр шеек коленчатого вала, м;  – расстояние между цилиндрами, м;  – коэффициент, вычисляемый по формуле  – для двигателя с чугунными поршнями и  – для двигателя с силуминовыми поршнями;  –  длина шатуна, м;  – количество цилиндров, работающих на одну шейку.

Рис. 5.26. Расчетные модели: а – простая; б – разветвленная; в – кольцевая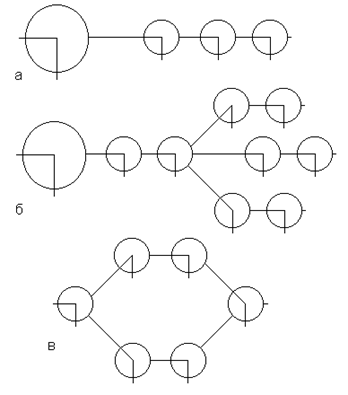

Область применения этой формулы 1,2 £ £ 3,8.

Более грубое приближение дает эмпирическая формула

,

где  – ход поршня, м;  – коэффициент, характеризующий тактность двигателя: для двухтактных ДВС 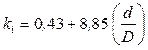; для четырехтактных ДВС, имеющих чугунные и силуминовые поршни, соответственно: 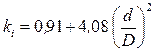 и 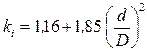;  – коэффициент, учитывающий конструкцию двигателя, для однорядных  = 1, для V-образных  = 1,3;  – коэффициент, учитывающий наличие противовесов, при отсутствии противовесов  = 1, а при их наличии  = 1,2¸2.