Основы проектирования и расчета судового валопровода, страница 21

Момент инерции валопровода определяют для каждого вала в отдельности. Полученное значение поровну сосредоточивают по концам вала.

Момент инерции массы цилиндрического вала длиной  с наружным и внутренним диаметрами соответственно  и  выражается известной зависимостью

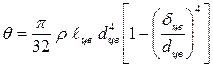                                 .                        (5.29)

Если участок между двумя сосредоточенными массами вала состоит из  цилиндрических элементов, то общий момент инерции участка будет

.

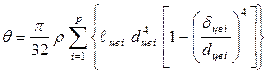Здесь  – плотность материала вала, для стали  = (7,7¸7,9)×10³ кг/м³.

Момент инерции гребного винта  при крутильных колебаниях увеличивается за счет массы увлекаемой им воды , поэтому в расчет вводится приведенный момент инерции гребного винта

                                         .                                       (5.30)

Для приближенного определения  и  применяют эмпирические формулы Кутузова:

;  ,

где  – диаметр гребного винта, м;  – шаг винта, м;  – дисковое отношение;  – коэффициент, вычисляемый по формуле .

Если параметры гребного винта неизвестны, то допустимо применять ориентировочную формулу, учитывающую массу увлекаемой воды

,

где  – мощность, потребляемая гребным винтом, кВт;  – частота вращения гребного винта, мин^-1;  – коэффициент, учитывающий конструкцию гребного винта: для ВФШ  = 7,75×10⁶, для ВРШ =12,65×10⁶.

Моменты инерции некоторых деталей (роторы электродвигателей, гребные винты, маховики) иногда характеризуются маховым моментом . Тогда, если маховой момент имеет единицу измерения кг×м², момент инерции определяется по формуле

.

Крутильную податливость (Н^-1×м^-1) валопровода подсчитывают раздельно для каждого вала. Ниже приведены формулы, по которым определяются крутильные податливости наиболее типичных элементов судового валопровода.

Крутильная податливость цилиндрического вала длиной , имеющего наружный  и внутренний  диаметры, вычисляется по формуле

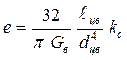                                          ,                                  (5.31)

где  – коэффициент сверления

;

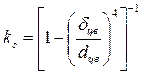 – модуль сдвига материала вала, связанный с модулем упругости  и коэффициент Пуассона  зависимостью

.

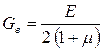Если вал имеет тонкостенную облицовку, то выражение принимает вид (рис. 5. 27,а)

.

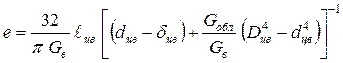Здесь  – модуль сдвига материала облицовки.

Крутильная податливость конического участка вала согласно обозначениям рис. 5.27,б определяется по формуле

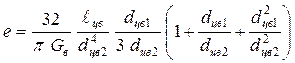                        .                (5.32)

При наличии сверления в (5.32) добавляется множитель .

Податливость фланцевого соединения (рис. 5.27,в) может быть подсчитана по выражению

.

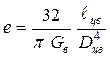Расчет суммарной податливости ступенчатого вала (рис. 5.27,г) производится по формуле

,

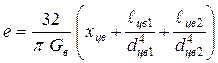где коэффициент  вычисляется

.

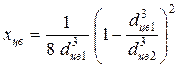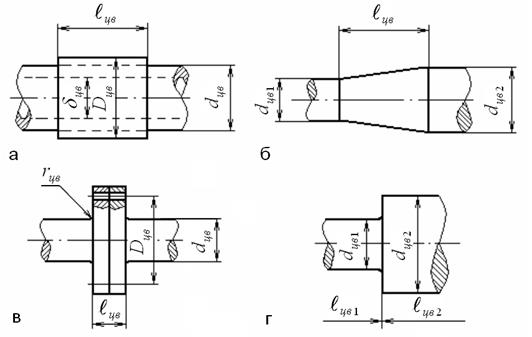
Рис. 5.27. Типичные элементы судового валопровода:                                                                                                                 а – вал с облицовкой; б – конический вал; в – фланцевое соединение                                           валов; г – ступенчатый вал

C учетом приведенных формул податливость вала определяется суммарной податливостью его отдельных участков, т.е. .

Для определения крутильной податливости колена вала имеется несколько формул, которые носят полуэмпирический характер и гарантируют результаты с погрешностью (5¸20)%. Формула Зиманенко дает наилучшее приближение к действительной податливости, найденной экспериментально, и пригодна для самых разнообразных двигателей:

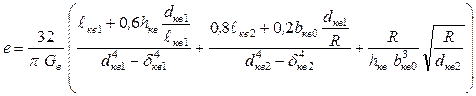. (5.33)

Формула Картера отличается простотой, она дает удовлетворительные результаты для коленчатых валов высокооборотных двигателей автотракторного типа

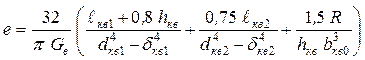                 .        (5.34)

Обозначения в формулах (5.33) и (5.34) показаны на рис. 5.28.

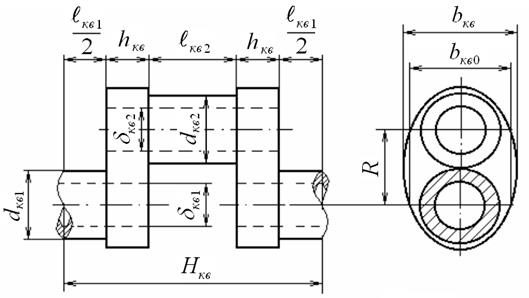
Рис. 5.28. Эскиз колена вала

Для грубого ориентировочного определения крутильной податливости можно пользоваться формулой Терских

,

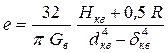где  и  – средние для шеек вала наружный и внутренний диаметры.

Для этой же цели может быть использована формула [19]:

,

пригодная для случая, когда  > 4 ( – диаметр цилиндра, м; – ход поршня, м).