Основы проектирования и расчета судового валопровода, страница 22

Податливость зубчатой передачи можно считать равной нулю в тех случаях, когда перекладка зазора между зубьями не имеет места. При больших колебаниях, когда амплитуда упругого момента больше среднего крутящего момента, передача приобретает нелинейные свойства жесткого соединения с зазором.

Податливость зубчатой передачи в тех случаях, когда перекладка зазора между зубьями отсутствует, определяют по формуле

,

где  – начальный диаметр колеса, к оси которого приводится податливость;  – ширина зубчатого венца;  – опытный коэффициент, для стальных колес  = 375×10⁷ Н/м².

Для вычисления крутильной податливости ременной и цепной передач можно пользоваться формулой

,

где  – жесткость ремня или цепи на растяжение;  – радиус ведомого шкива или звездочки;  = 1 для цепной и  = 2 для переменной передач.

Крутильную податливость упругих муфт принимают по паспортным данным. Такие муфты часто оказываются наиболее податливыми элементами валопровода.

Электрическая связь между ротором генератора и ротором электромотора на постоянном токе эквивалентна бесконечной податливости; то же самое имеет место при включении в систему валопровода электроиндукционной или гидравлической муфты. В расчетах  эти системы можно считать изолированными одна от другой. Электрическая связь на переменном токе характеризуется конечной податливостью.

5.10.3. Методы расчета свободных                                             крутильных колебаний

Для составления дифференциальных уравнений свободных крутильных колебаний обычно пользуются уравнениями Лагранжа второго рода.

Применительно к дискретной разветвленной модели, состоящей из  масс и изображенной на рис. 5.29, уравнения Лагранжа имеют вид

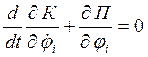                                  ,     1, 2, …,          (5.35)

где  и  – соответственно, кинетическая и потенциальная энергия рассматриваемой модел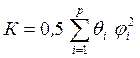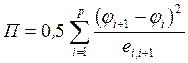и:

;   ,

и  – скорость поворота и угол отклонения массы от равновесного состояния.

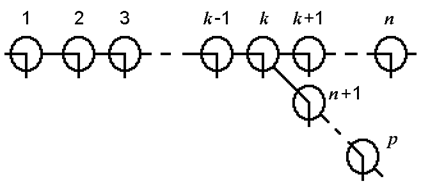
Рис. 5.29. Разветвленная расчетная модель

После подстановки выражений для  и  в (5.35) получим искомую систему уравнений свободных колебаний

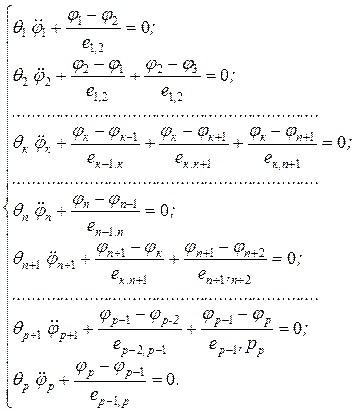
Значительно компактнее запись этих уравнений выглядит в матричной формуле

                                       ,                            (5.36)

где  – диагональная матрица моментов инерции

;

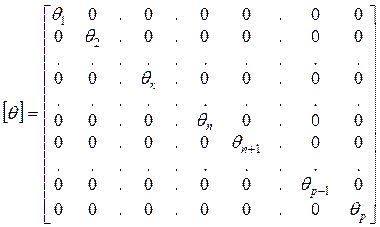 – квадратная матрица жесткости (ее коэффициенты – величины, обратные податливости соединения ), приведена на следующей странице;  и  – матрицы-столбцы деформаций и ускорений:

;  .

В теории колебаний доказано, что решение системы (5.36) следует искать в форме гармонических функций

                                      ,                              (5.37)

где  – амплитуда колебаний, рад;  – круговая частота свободных колебаний, с^-1;   – начальная фаза, рад.

Связь между круговой частотой  и технической частотой  (Гц) устанавливает зависимость

.

Подставив (5.37) в (5.36), получим систему алгебраических уравнений, которая в матричной форме примет вид

                                       .                             (5.38)

Система (5.38) имеет нулевые решения в двух случаях. Первый случай соответствует состоянию валопровода, который находится в покое и колебания отсутствуют, т.е. = 0. Второй случай имеет место при условии, что ее определитель равен нулю:

                                             .                              (5.39)

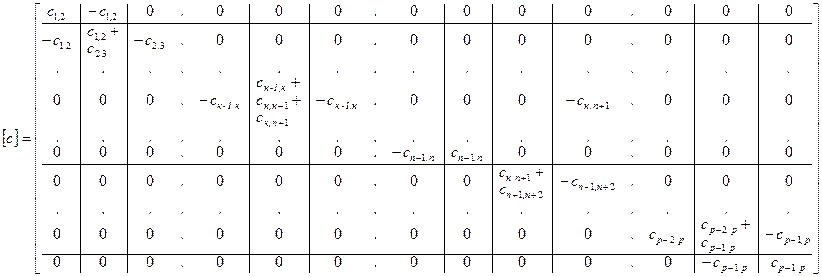
Уравнение (5.39) называется частотным уравнением, оно позволяет найти все частоты свободных колебаний. Для его решения часто используется итерационная процедура анализа числа знакоперемен определителя (5.39) в функции . Последний предварительно приводится к треугольному виду в результате прямого хода по методу Гаусса. Условием нахождения собственной частоты в интервале шага итерации является изменение знака определителя. При выполнении этого условия частота свободных колебаний уточняется до тех пор, пока не будет достигнута заданная точность. После этого решается система (5.39) и определяются амплитуды колебаний всех масс. Эта операция использует обратный ход метода Гаусса. Здесь следует отметить, что ввиду однородности уравнений (5.38) одна из амплитуд остается неопределенной, поэтому вычисляются не сами амплитуды, а их отношения к амплитуде колебаний (обычно первой массы). Эти отношения называются безразмерными амплитудами: