Основы проектирования и расчета судового валопровода, страница 19

В практических расчетах свободных изгибных колебаний судовых валопроводов наибольшее распространение получили два метода.

В методе, предложенным.Ю.А. Шиманским, валопровод идеализируется многопролетной статически неопределимой балкой. При изгибных колебаниях этой балки каждый из ее пролетов совершает такие же колебания, как и двухопорная балка с упругозащемленными концами (рис.7.22). При такой форме колебаний прогибы смежных пролетов неразрезной балки направлены в противоположные стороны. Возникающие при этом опорные моменты , пропорциональные углам поворота надопорного сечения , принимаются с противоположными знаками для пролетов, расположенных по разные стороны от каждой опоры. Это равносильно тому, что коэффициенты жесткости изгибу опорного сечения балки будут одинаковыми по абсолютной величине, но разными по знаку.

Таким образом, свободные колебания неразрезной балки можно рассматривать в виде совокупности колебаний всех ее пролетов с одинаковой частотой. Колебания каждого пролета рассматриваются как колебания однопролетной балки с соответствующими закреплениями ее концов (определенными коэффициентами жесткости), отвечающими условиям вхождения в состав многопролетной балки.

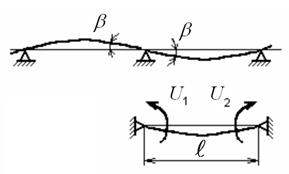
Рис. 7.22. Деформации неразрезной балки

Изложенное представляет собой словесный алгоритм расчета. Его основу составляют рекуррентные формулы, устанавливающие зависимость коэффициентов изгибной жесткости на левом конце пролета от коэффициентов жесткости на правом конце смежного с ним пролета.

Изложенный алгоритм позволяет находить низшую частоту свободных изгибных колебаний. Однако не исключена возможность определения и других частот. Это основано на том, что каждой частоте свободных колебаний присуща своя форма. На рис. 7.23 представлены две формы колебаний, соответствующие частотам  и , причем . Видно, что отличие в формах колебаний заключается в появлении других дополнительных узлов, т.е. сечений, не участвующих в колебаниях. Таким образом, вводя дополнительные фиктивные опоры в расчетную модель, можно определить частоту любой формы свободных изгибных колебаний валопровода.

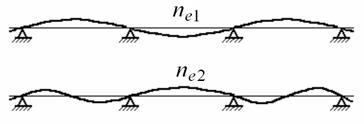
Рис. 7.23. Формы изгибных колебаний

Во втором методе, разработанном сотрудниками ЦНИИ им. акад. А.Н.Крылова, при расчете изгибных колебаний рассматривают только кормовой участок валопровода, и поэтому расчетная схема представляется в виде обыкновенной статически определимой балки, покоящейся на двух точечных опорах. При данных условиях низшую частоту свободных изгибных колебаний судового валопровода в вертикальной плоскости  (Гц) ориентировочно можно определить по формуле

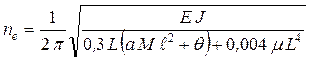                        ,            (5.25)

где  – модуль упругости материала вала, для стали  = 2,1×10¹¹ Па; – осевой момент инерции опасного сечения гребного вала, м⁴;  и – масса (кг) и момент инерции массы (кг×м²) гребного винта;  – погонная масса гребного вала, кг×м^-1;  и  – длина консоли и кормового пролета гребного вала, м (рис. 5.24);  – безразмерный коэффициент, характеризующий податливость дейдвудных подшипников:  = 1,5 – для металлических подшипников,  = 2,5 – для бакаутовых и текстолитовых подшипников,  = 4 – для резинометаллических и капролоновых подшипников.

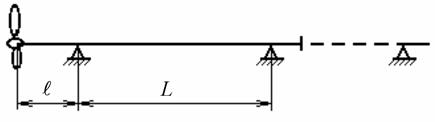
Рис. 5.24. Расчетная модель гребного вала

При отсутствии конструктивных данных допускается вычислять массу и момент инерции гребного винта по формулам (5.10) и (5.30), соответственно.

Точность расчета по (5.25) существенно зависит от величины . При достаточной длине пролета  ³ 10 ( – диаметр гребного вала) расчетные и опытные данные хорошо согласуются и погрешность не превышает 15% [1]. При близком расположении подшипников гребного вала (< 10) формула (5.25) дает завышенные результаты. Исключение же из расчета носовой опоры гребного вала вообще приводит к заниженным результатам. В этом случае расчетную величину частоты свободных колебаний рекомендуется определять как среднее между указанными значениями по формуле

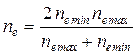                                          .                               (5.26)