Основы проектирования и расчета судового валопровода, страница 27

Расчеты колебаний с использованием приведенного коэффициента поглощения не требуют каких-либо корректировок процедуры определения демпфирующего момента. Его величина может быть подсчитана непосредственно через энергию рассеяния, а в случае вязкого трения – посредством коэффициента пропорциональности. Для резонансного режима

,

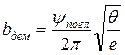где  и  – момент инерции массы и крутильная податливость участка вала.

Приведенный коэффициент поглощения энергии получают экспериментальным путем. С этой целью выполняется торсиографирование или тензометрирование судового валопровода, и по их результатам строится амплитудно-частотная характеристика. Обработка последней по высоте или ширине  резонансного пика дает искомое значение коэффициента поглощения.

5.10.7. Расчет резонансных колебаний

В теории колебаний показано, что при резонансе работа вынуждающих моментов полностью расходуется на преодоление моментов сил трения. Это положение составляет основу энергетического метода, общепризнанного в расчетах резонансных колебаний судовых валопроводов. Другими словами, при резонансе соблюдается равенство между работами вынуждающих и демпфирующих моментов

.

В энергетическом методе помимо указанного равенства используется другая закономерность резонансных колебаний, а именно – совпадение форм свободных и резонансных колебаний. Наличие такого совпадения позволяет вычислить действительные амплитуды колебаний всех масс дискретной модели, если известна амплитуда одной, например, первой массы. Связь между действительными и безразмерными амплитудами устанавливается соотношением

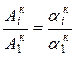                                    ,  .                           (5.45)

Отмеченные выше предпосылки энергетического метода определяют алгоритм расчета резонансных колебаний. Суть его состоит в следующем. Сначала подсчитывается работа, которую совершают вынуждающие моменты в процессе колебаний. При этом рассматривают только те гармонические составляющие, которые вызывают резонансный режим. Затем для частоты резонансных колебаний вычисляется энергия диссипации. Работу и энергию определяют обычно за один цикл колебаний, равный периоду 2p. Далее из баланса полученных величин находят амплитуду колебаний первой массы. После этого, пользуясь соотношением (5.45), устанавливают действительные амплитуды колебаний всех остальных масс. Напряжения от крутильных колебаний в любом соединении дискретной модели вычисляют по формуле

.

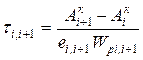Допустимые напряжения регламентируются Правилами Российского морского регистра судоходства.

Ниже приведены расчетные зависимости энергетического метода.

В случае действия на дискретную массу с номером  гармонического момента -го порядка работа, совершаемая им за период 2p, равна

                                        .                            (5.46)

Суммарная работа гармонических моментов того же порядка на всех кривошипах коленчатого вала

.

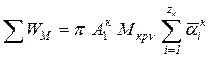Множитель 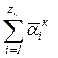 называют геометрической суммой безразмерных амплитуд. Ее величину можно определить графическим построением. Для этого в некотором масштабе производят геометрическое суммирование безразмерных амплитуд, направляя их как векторы параллельно лучам фазовой диаграммы -го порядка. Такая диаграмма строится на основании порядка вспышек в цилиндрах двигателя и углов заклинивания кривошипов коленчатого вала. Углы между лучами фазовой диаграммы

,

где  – начальная фаза заклинивания -го кривошипа, соответствует углу между первым и -м кривошипом, замеренному в направлении вращения коленчатого вала.

Для главных порядков векторное суммирование переходит в алгебраическую сумму безразмерных амплитуд. Поскольку алгебраическая сумма больше геометрической, работа вынуждающих моментов главного порядка всегда будет максимальной.

При использовании ЭВМ геометрическую сумму безразмерных амплитуд вычисляют аналитическим способом. Структура расчетной формулы полностью сохраняет особенности геометрического суммирования, но выраженного через проекции векторов. На этом  основании