|
Материал подшипника |
Износ (мм) за 1000 ч ходового времени |
|
Бакаут Резина Древесно-слоистый пластик Баббит |
0,22 0,15 0,22 0,002 |
В зависимости от способа присоединения валопровода к двигателю балку считают либо жестко защемленной, либо свободно опертой. Первая схема идеализации справедлива для случая присоединения вала непосредственно к фланцу отбора мощности, а вторая соответствует наличию упругой муфты в этом соединении.
В качестве расчетных нагрузок принимают все силы и моменты, действующие в вертикальной плоскости, а именно: силы тяжести гребного винта и сосредоточенных масс валопровода; распределенную нагрузку валов; вертикальную составляющую гидродинамического изгибающего момента.
Расчет опорных реакций выполняется чаще всего с помощью уравнений трех моментов, каноническая запись которых имеет вид
![]() . (5.12)
. (5.12)
Алгоритм формирования уравнений включает в себя следующие операции. Предварительно:
– консольные участки балки отбрасываются, а их действие компенсируется силой и моментом;
– защемление балки заменяется дополнительным бесконечно малым пролетом;
– опоры и пролеты последовательно нормируются, причем первой опоре присваивается номер ноль (рис. 5.16).
Далее следуют вычислительные процедуры, в результате которых подсчитываются:
– приведенные длины пролетов (![]() = 1,
2,…)
= 1,
2,…)
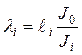 ,
,
где ![]() и
и ![]() – длина
и осевой момент инерции поперечного сечения i-го пролета;
– длина
и осевой момент инерции поперечного сечения i-го пролета; ![]() – постоянная балки (момент инерции любого
пролета);
– постоянная балки (момент инерции любого
пролета);
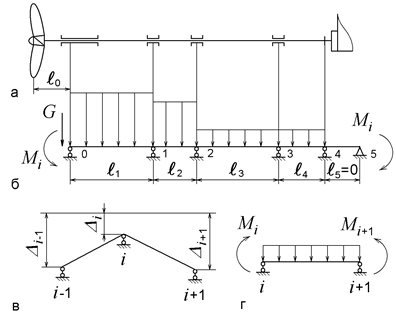
Рис. 5.16. Идеализация валопровода: а – конструктивная схема; б – расчетная модель; в – смещение опор; г – однопролетная балка
– коэффициент внешней нагрузки
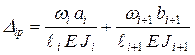 , (5.13)
, (5.13)
где ![]() и
и ![]() –
площади эпюр изгибающих моментов, соответственно, в
–
площади эпюр изгибающих моментов, соответственно, в ![]() -м и (
-м и (![]() +1)-м пролетах;
+1)-м пролетах; ![]() и
и ![]() расстояния от центра тяжести эпюры до
левой и правой опор;
расстояния от центра тяжести эпюры до
левой и правой опор; ![]() – модуль упругости при растяжении.
– модуль упругости при растяжении.
Значения ![]() ,
, ![]() и
и ![]() для
некоторых видов нагрузки приведены в табл.5.5. Если эпюры изгибающих моментов в
однопролетных балках представляют собой сложные фигуры, то их следует расчленить
на ряд простых. В этих случаях в (5.13) вместо выражений
для
некоторых видов нагрузки приведены в табл.5.5. Если эпюры изгибающих моментов в
однопролетных балках представляют собой сложные фигуры, то их следует расчленить
на ряд простых. В этих случаях в (5.13) вместо выражений ![]() и
и ![]() подставляются
подставляются
![]() и
и ![]() ;
;
– коэффициент, учитывающий смещение опор
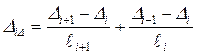 ,
,
где ![]() ,
, ![]() и
и ![]() – смещение опор (рис. 5.16,в).
– смещение опор (рис. 5.16,в).
Следующая операция – составление и решение системы алгебраических уравнений, как правило, методом Гаусса. В результате получают надопорные изгибающие моменты М для всех промежуточных опор. Положительные направления моментов показаны на рис. 5.16,г. После этого каждый пролет рассматривают как простую балку на двух опорах, нагруженную заданной внешней нагрузкой и надопорными моментами. Для такой балки поперечную силу и изгибающий момент в любом сечении подсчитывают по формулам
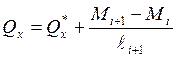 ;
;
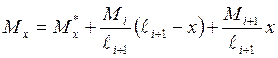 ,
,
где ![]() и
и ![]() –
поперечная сила и изгибающий момент в простой балке от внешней нагрузки (см.
табл. 5.5).
–
поперечная сила и изгибающий момент в простой балке от внешней нагрузки (см.
табл. 5.5).
Из выражения для поперечных сил легко найти реакции опор
![]() .
.
Соответствующие ![]() удельные давления в
подшипниках
удельные давления в
подшипниках
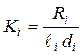 , (5.14)
, (5.14)
где ![]() – длина вкладыша;
– длина вкладыша; ![]() – диаметр шейки.
– диаметр шейки.
На основе рассмотренного алгоритма удается сделать предложения, касающиеся равномерной нагрузки подшипников. Для этого выполняют итерационные расчеты, в которых путем вертикального смещения опор добиваются перераспределения реакций. Такая оптимизационная задача обязательно решается всегда, когда отдельные опоры оказываются малонагруженными или имеют отрицательные реакции, а также при наличии большого надопорного момента в месте защемления балки. Данный момент дополнительно изгибает коленчатый вал дизеля или выходной вал редуктора, поэтому его значение должно быть минимальным.
Задачу по определению реакций опор можно решить также методом конечных элементов. Наиболее просто построить стержневую конечноэлементную модель. Для этого достаточно выбрать определенное число узлов вдоль оси валопровода и соединить их прямыми линиями. Благодаря возможности варьировать расстояние между узлами, учитывать податливость опор и идеализировать подшипники элементами конечной длины, удается учесть конструктивные особенности валов. Кроме того, при использовании метода конечных элементов отпадает необходимость в замене консоли и защемления соответствующими усилиями и дополнительным пролетом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.