Основы проектирования и расчета судового валопровода, страница 13

С учетом изложенного наибольшее значение изгибающего момента определяется зависимостью

      .   (5.16)

Формула (5.16) включает в себя гидродинамические составляющие изгибающего момента в двух взаимоперпендикулярных плоскостях, момент от силы тяжести гребного винта, момент от волнения моря, коэффициенты динамичности для лопастей частоты  и , соответственно, в вертикальной и горизонтальной плоскостях, а также коэффициент динамичности  для частоты, совпадающей с частотой вращения гребного винта. На стадии эскизного проектирования значения коэффициентов динамичности принимают в пределах =1,4¸1,7; =1,2¸1,5;  = 1,1¸1,4.

Напряжения от изгибающего момента

,

где  – осевой момент сопротивления опасного сечения гребного вала

.

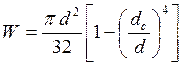Аналогичным образом вычисляются напряжения от упора и крутящего момента. Максимальная величина силы, вызывающей деформацию сжатия гребного вала

.

Соответствующие этой силе напряжения

,

где  – площадь поперечного сечения гребного вала.

Напряжения от крутящего момента

.

Здесь  – максимальное значение крутящего момента

.

Таким образом, рассматриваемое сечение гребного вала испытывает сложное напряженное состояние, которое характеризуется  одновременным действием нормальных и касательных напряжений. В этих условиях предсказать вероятность разрушения вала невозможно и обычно для решения поставленной задачи пользуются какой-либо гипотезой прочности. На базе ее устанавливается соответствие между фактическими деформациями и одноосным растяжением. Например, напряжения в опасном сечении гребного вала по энергетической гипотезе составляют

                                                             (5.17)

Сопротивление этих напряжений с пределом текучести дает запас прочности. Минимально допустимая величина запаса статической прочности для судовых валопроводов составляет 1,5.

5.6.3. Расчет на выносливость

В результате длительного действия переменных напряжений происходит зарождение и развитие усталостных трещин. Среди отличительных особенностей этого явления заслуживают внимания следующие:

– усталостные поломки наблюдаются при напряжениях намного ниже тех, которые приводят к разрушению в статических условиях;

– свойства материала в процессе усталости практически не меняются, поэтому трудно обнаружить признаки прогрессирования трещин;

– повреждения при усталости являются необратимыми.

Несмотря на то, что усталость представляет собой довольно сложный механизм разрушения, она прогнозируется при проектировании валопроводов в расчетах на выносливость. Цель расчета – определение коэффициента запаса прочности, посредством которого можно делать определенные суждения о долговечности валов при действии пульсирующих усилий. Долговечность обычно ассоциируется с числом 10⁷¸10⁸ циклов нагружения до разрушения.

Проблема расчета на выносливость включает в себя решение, по крайней мере, трех основных задач.

Первая связана с выяснением цикла изменения напряжений, т.е. установлением максимальных и минимальных напряжений. При этом функциональная зависимость напряжений от времени предполагается синусоидальной. Знание экстремальных напряжений позволяет вычислить среднее значение и амплитуду цикла:

;   .

Такой подход к решению задачи представляется весьма упрощенным и справедливым только для не вращающегося вала. В реальных условиях цикл изменения напряжений определяется характером действия внешней нагрузки и взаимным положением ее и вала. Например, силы тяжести обусловливают постоянные напряжения, однако при вращении вала они изменяются по симметричному циклу. Действие переменного крутящего момента вызывает в сечениях вала ассиметричный цикл изменения напряжений. Упор создает напряжения сжатия, ввиду их благоприятного воздействия на предел выносливости и невысокий уровень, ими, как правило, пренебрегают. Отмеченные закономерности позволяют записать следующие зависимости для интересующих величин

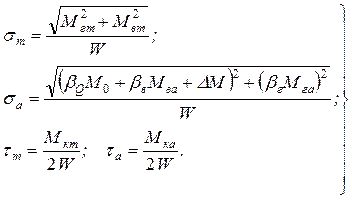                            (5.18)