Основы проектирования и расчета судового валопровода, страница 24

,  .

Частоты свободных колебаний подвергают анализу на установление резонансных режимов эксплуатации судового движительного комплекса. По амплитудам колебаний масс строят формы колебаний. Для этого их откладывают (с учетом знака) под расчетной моделью в виде пропорциональных ординат. Формы колебаний различаются по числу узлов, т.е. по числу перемен знака у амплитуд. Между числом узлов и порядковым номером частоты свободных колебаний существует строгое равенство. Так, одноузловая форма свободных колебаний соответствует только низшей частоте , двухузловая форма присуща второй частоте  и т.п.

Форма свободных колебаний позволяет установить те участки валопровода, которые имеют наибольшую интенсивность колебаний. Однако практический интерес с точки зрения динамической прочности имеют величины касательных напряжений в сечениях валопровода, вызванные данными колебаниями.

Если бы все участки вала представляли собой отрезки одного диаметра, то напряжения в них были бы пропорциональны найденным амплитудам упругих сил . В действительности, моменты сопротивления сечения вала  на большей части участков различны. Поэтому, вводится так называемый масштаб напряжений, представляющий собой отношение амплитуды напряжений  к амплитуде колебаний какой-либо массы, например, первой:

.

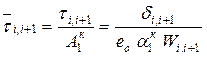где  – полярный момент сопротивления соединения .

Подсчет  для всех участков валопровода позволяет найти тот из них, где наблюдаются наибольшие амплитуды касательных напряжений. Действительные значения этих напряжений можно определить только после расчета резонансных колебаний.

5.10.4. Построение частотной диаграммы

Выше отмечалось, что наибольшую опасность для прочности валопровода представляют резонансные режимы эксплуатации. Это обстоятельство заставляет выявлять такие режимы заблаговременно путем построения частотной диаграммы (рис. 5.30).

Частотную диаграмму строят в прямоугольной системе координат: по оси ординат откладывают частоты колебаний (Гц), по оси абсцисс – частоты вращения гребного винта или коленчатого вала (с^-1). Горизонтальными линиями на диаграмме отмечают частоты свободных колебаний, а лучами в виде пучка прямых – частоты вынуждающих моментов. Точки пересечений лучей с горизонтальными линиями указывают на резонансы частоты вращения.

Анализ вынуждающих моментов как со стороны ДВС, так и гребного винта показывает, что частоты их изменения  пропорциональны частоте вращения вала . Следовательно, частота вынужденных колебаний , где  – порядок гармонической составляющей.

Для ДВС порядок гармоники кратен числу вспышек за один оборот коленчатого вала. Поэтому в двигателях, работающих по четырехтактному циклу, возможны следующие порядки:

 Î (0,5; 1; 1,5; 2; 2,5; 3; 3,5;…).

В двухтактном двигателе

 Î (1; 2; 3; 4; 5; 6; 7;…).

Среди указанных порядков наиболее опасными являются главные порядки. В двухтактном ДВС главный порядок равен числу цилиндров двигателя, а в четырехтактном – числу цилиндров, деленному пополам.

Для гребного винта практический интерес представляют только колебания с частотой, равной частоте вращения гребного винта =1, и колебания с лопастной частотой, порядок которых кратен числу лопастей винта :  = ;  = 2;  = 3;  = 4.

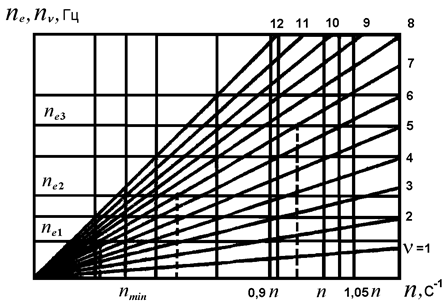
Рис. 5.30. Частотная диаграмма

5.10.5. Определение вынуждающих моментов

При работе дизеля каждый кривошип коленчатого вала подвергается действию переменных нагрузок. Тангенциальная сила  (одна из таких нагрузок) определяет крутящий момент, который передается коленчатому валу и возбуждает в нем крутильные колебания. Величина этой силы, отнесенная к площади поршня, вычисляется в динамическом анализе кривошипно-шатунного механизма. С учетом отмеченного крутящий момент

,

где  – радиус кривошипа;  – площадь поршня.