Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 9

В описываемом ниже примере текста программы численного интегрирования системы дифференциальных уравнений заложено решение в течение половины секунды следующей системы уравнений:

.

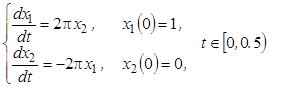Аналитическим решением этой системы являются функции  и . Численный метод Рунге-Кутта имеет погрешность, пропорциональную четвертой степени шага по независимой переменной. При шаге h=0.1 ошибка будет иметь порядок  . Чтобы повысить точность результата решения на порядок необходимо уменьшить шаг в 10 раз. При этом для просмотра всего заданного интервала в одну секунду придется выводить в 10 раз больше векторов решения, так как число точек на оси времени возрастет в те же 10 раз, особого смысла в которых нет.

Идея вывода нужного числа векторов решения в нужные моменты времени, например, через интервалы, равные десяти кратно увеличенному шагу, необходимо после каждых k=10 циклов выполнения процедуры RK(*) вывести последний вектор на печать, его значение присвоить вектору начальных условий v0 и снова 10 раз выполнить процедуру RK(*). Эти действия для охвата заданного интервала решения необходимо повторить m=5 раз.

Таким образом, в тексте программы, кроме задания системы уравнений, вектора решения и его начального значения, должен присутствовать оператор с двумя вложенными циклами. Один (внутренний), соответствующий собственно процедуре Рунге-Кутта, повторяющийся k раз, и внешний – для повторной подстановки очередного вектора начальных значений и вывода промежуточных подстановок начальных векторов.

Если файл разработанной программы содержит процедуры из какой-либо утилиты, то первой строчкой программы желательно иметь напоминание о том, какая утилита должна быть предварительно загружена, прежде чем загружать программу. Такое напоминание выполняется текстом с латинскими буквами, взятым в двойные кавычки.

#1   "LOAD(Ode_appr.mth)"”

#2   u:=[2·¹·x2, -2·¹·x1]

#3   v:=[t, x1, x2]

#4   v0:=[0, 1, 0]

#5   Frk(h,k,m):=ITERATES((RK(u,v,in,h,k))   ,in,v0,m)

                                 k+1        

#6   F(h,k,m):=APPEND([v],Frk(h,k,m))

#7   Sin:=APPEND(["sin(2¹t)"],VECTOR(SIN(2·¹·t),t,0,0.5,0.1))

#8   APPEND(F(0.01,10,5)`,[Sin])`

„  t        x1               x2          "sin(2¹t)"   †

¦                                                     ¦

¦  0         1                0                0      ¦

¦                                                     ¦

¦ 0.1  0.8090170388     -0.5877851838    0.5877852522 ¦

#9  ¦                                                     ¦

¦ 0.2  0.3090171467     -0.9510564578    0.9510565162 ¦

¦                                                     ¦

¦ 0.3  -0.3090167610    -0.9510565898    0.9510565162 ¦

¦                                                     ¦

¦ 0.4  -0.8090167975    -0.5877855123    0.5877852522 ¦

¦                                                     ¦

¦                                    -7               ¦

… 0.5       -1        -4.075748779·10          0      ‡

В приведенном тексте программы первый оператор напоминает о необходимости загрузить файл, содержащий утилиту с процедурой Рунге-Кутта. Операторы 2-4 определяют значения фактических параметров для процедуры RK(*), входящей в выражение функции Frk(h,k,m). Имя функции через список параметров позволяет задавать нужные фактические параметры: шаг по времени h, кратность шагу по времени k, определяющую моменты вывода векторов решения, и общее число выводимых векторов m. Основой функции является оператор ITERATES(), который последовательно m раз изменяет значение n-мерного вектора v0 (n=3) в процедуре RK(*). Сама процедура вычисляет k раз 3-мерный вектор v, формируя скрытый (k+1)-мерный вектор промежуточных значений вектора v. Индекс (k+1) при процедуре выделяет из k циклов ее работы (k+1)-ю (то есть последнюю) векторную компоненту, после чего оператор итерационной подстановки присваивает ее вектору v0 и выводит в очередную строку таблицы результата оцифрованные значения переменных.