Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 24

IF(Rzn(j,n)=?,"",Rzn(j,n))

Теперь вектор разделенных разностей всех возможных порядков для n-ой строки табличной функции можно представить так:

Vrzn(n):=VECTOR(IF(Rzn(j,n)=?,"",Rzn(j,n)),j,0,5)

Перечисление всех подобных строк сделает оператор

VECTOR(Vrzn(n),n,0,5)

„  -0.06   1.20666   -1.57777   0.712962   -0.366512  0.248628 †

¦  0.664  -0.686666  -0.294444  -0.166666  0.379372      ""    ¦

¦  0.252    -1.04    -0.594444  0.743827      ""         ""    ¦

¦ -0.372  -1.75333   0.744444      ""         ""         ""    ¦

¦ -1.424    -0.86       ""         ""         ""         ""    ¦

…  -1.94     ""         ""         ""         ""         ""    ‡

В полученной таблице разделенных разностей не хватает столбца аргументов и строки заголовков. Последнюю представим вектором

Zg:=[x,f,[x0,x1],[x0,...,x2],[x0,...,x3],[x0,...,x4],[x0,...,x5]]

Оператор, объединяющий заголовок, столбец аргументов и таблицу разностей, получит следующий, окончательный вид:

Tr:=APPEND([Zg],APPEND(„g †,VECTOR(Vrzn(n),n,0,5)`)`)

                       … 1‡                          

Проверка вычисления [x0,...,x3] для 2-й строки

-0.594444-(-0.294444)

————————————————————- = -0.166666

       3.1-1.3       

Задача №6: Полиномы Лагранжа и Ньютона

Получить интерполяционные многочлены Лагранжа и Ньютона, проходящие через первые четыре точки таблично заданной g(x), и сравнить их степенные представления.

Интерполяционные многочлены Лагранжа и Ньютона

Формула интерполяционного многочлена Лагранжа степени n:

.

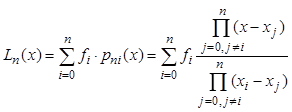Формула интерполяционного многочлена Ньютона степени n:

,

где          – многочлен степени n, кривая которого пересекает ось абсцисс только в n точках ();

                – повторная разделенная разность n порядка.

Построение операторов для формирования многочленов

Чтобы построить оператор Лагранжа, сначала построим произведения скобочных форм, из которых выбрасывалась бы одна скобка с вычитаемой величиной заданного индекса.  ¹

Команды, формирующие произведения разностных сомножителей для числителя и знаменателя формулы Лагранжа, имеют следующие тексты:

£(IF(j ¹ i, x - tr™(2 + j)™1, 1), j, 0, n)

£(IF(j ¹ i, tr™(2 + i)™1 - tr™(2 + j)™1, 1), j, 0, n)

После выполнения этих команд их формульные представления делим одно на другое и домножаем на значение i-той ординаты табличной функции.

Полученное таким образом формульное представление i-того слагаемого для формулы Лагранжа подставляем в оператор суммирования с пределами суммирования по i от 0 до n:

                 n                         

                 £  IF(j¹i,x-Tr     ,1)    

 n              j=0            2+j,1       

 ¤  Tr     ·——————————————————————————————-

i=0   2+i,2   n                            

              £  IF(j¹i,Tr     -Tr     ,1)

             j=0          2+i,1   2+j,1    

В соответствии с заданием интерполяционный многочлен Лагранжа необходимо построить таким, чтобы он проходил через первые 4 точки таблично заданной функции. Подставив в выражение суммы n=4 и исполнив его, получим после приведения к степенной форме, следующий полином:

          3            2                      

0.712962·x  - 4.35832·x  + 7.72027·x - 3.57315

Проверка правильности многочлена Лагранжа

Так как интерполяционный многочлен обязан пройти через заданные точки, то вместе с графическим представлением полученного многочлена нанесем и заданные точки табличной функции. Выделим эти 4 точки из исходной таблицы Tr следующим оператором:

VECTOR(VECTOR(Tr   ,j,1,2),i,2,5)

                i,j              

„ 0.7   -0.06 †

¦ 1.3   0.664 ¦

¦ 1.9   0.252 ¦

… 2.5  -0.372 ‡

В графическом режиме выполняем полученный многочлен и табличку с координатами точек. Результирующий график показан на рисунке.

Операторы для интерполяционного многочлена Ньютона