Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 20

Задача 2:Повторные конечные разности.

Для функции g(x), заданной своими значениями в шести точках, составить таблицу всех повторных разностей. Преобразовать функцию g(x) с помощью линейного преобразования  в функцию G(k) с целочисленным аргументом k. Для проверки правильности заполнения таблицы вычислить аналитически конечную разность  для n=5.

Решение задачи для варианта №…

Таблично заданная функция g(x) определена так:

      „  0.7    1.3    1.9     2.5     3.1    3.7  †

g(x):=¦                                            ¦

      … -0.06  0.664  0.252  -0.372  -1.424  -1.94 ‡

Добавим в табличную функцию g(x) строку целочисленного аргумента, который нумерует заданные точки аргумента x , начиная с нуля, и является индексом для x. При этом между переменной x и целочисленной переменной i будет установлено соотношение   x=x₀+h·i=0.7+0.6·i:

G:=APPEND([VECTOR(i,i,0,5)],g(x))

   „   0      1      2       3       4      5   †

G:=¦  0.7    1.3    1.9     2.5     3.1    3.7  ¦

   … -0.06  0.664  0.252  -0.372  -1.424  -1.94 ‡

Повторная конечная разность n-го порядка таблично заданной функции сцелочисленным аргументом  определяется для каждого i следующими способами:

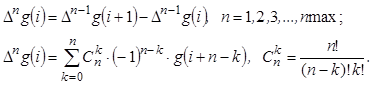
Первое определение позволяет последовательно вычислить конечные разности, начиная с конечных разностей нулевого порядка .

Выражение суммы включает (n+1) знакопеременное значение табличной функции, начиная с i-той точки, которые умножаются на коэффициенты, равные числу сочетаний из n элементов по k.

Построение таблицы повторных разностей для G(i) и G(x) по первому варианту:

kr1:=VECTOR(IF(i<DM(G )-0,G     -G   ,""),i,1,DM(G ))

                     3     3,i+1  3,i             3  

kr2:=VECTOR(IF(i<DM(G )-1,kr1   -kr1 ,""),i,1,DM(G ))

                     3       i+1    i             3  

kr3:=VECTOR(IF(i<DM(G )-2,kr2   -kr2 ,""),i,1,DM(G ))

                     3       i+1    i             3  

kr4:=VECTOR(IF(i<DM(G )-3,kr3   -kr3 ,""),i,1,DM(G ))

                     3       i+1    i             3  

kr5:=VECTOR(IF(i<DM(G )-4,kr4   -kr4 ,""),i,1,DM(G ))

                     3       i+1    i             3  

Здесь путем вычитания двух конечных разностей меньшего порядка в точках (i+1) и i формируются векторы из разностей на единицу более высокого порядка. При переходе к очередному порядку разностей количество значащих разностей в векторе уменьшается на единицу. Все разности, не имеющие значения для заданной табличной функции, с помощью условного оператора заменяются на символ из двух кавычек. Длина таблицы определяется здесь переопределенным именем оператора размерности вектора:     DM(v_):=DIMENSION(v_).

Для придания таблице конечных разностей заголовка заготовим вектор из переменных, которым численные значения в задаче не присваивались, иначе их необходимо заключить в двойные кавычки.

    „         2  3  4  5†

zg:=…k,x,f,, , , , ‡

Оператор таблицы соединяет воедино все полученные ранее векторы, представленные матрицами с векторными компонентами одного размера:

APPEND([zg],APPEND(G,[kr1],[kr2],[kr3],[kr4],[kr5])`)

„                            2       3      4      5  †

¦ k   x      f                                   ¦

¦ 0  0.7   -0.06   0.724  -1.136   0.924  -1.14  2.32 ¦

¦ 1  1.3   0.664  -0.412  -0.212  -0.216  1.18    ""  ¦

¦ 2  1.9   0.252  -0.624  -0.428   0.964   ""     ""  ¦

¦ 3  2.5  -0.372  -1.052   0.536    ""     ""     ""  ¦

¦ 4  3.1  -1.424  -0.516    ""      ""     ""     ""  ¦

… 5  3.7   -1.94    ""      ""      ""     ""     ""  ‡

Проверка

Для проверки правильности построенной таблицы получим ее же, используя второй способ вычисления конечных разностей. Для этого будем использовать уже определенные выше векторы G и zg . Число сочетаний из m компонент по k в DERIVE вычисляет оператор COMB(m,k).

         m      m-k